题目内容
已知双曲线 的两焦点为F1,F2,P为动点,若PF1+PF2=4.
的两焦点为F1,F2,P为动点,若PF1+PF2=4.(Ⅰ)求动点P的轨迹E方程;
(Ⅱ)若A1(-2,0),A2(2,0),M(1,0),设直线l过点M,且与轨迹E交于R、Q两点,直线A1R与A2Q交于点S.试问:当直线l在变化时,点S是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.
【答案】分析:(I)根据双曲线的方程为: -y2=1,则|FF2|=2
-y2=1,则|FF2|=2  ,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
(II)对于存在性问题,可先假设存在,假设存在满足条件的直线l在变化时,点S是否恒在一条定直线上,设直线a的方程为x=my+1,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用条件即可求得直线的方程,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(Ⅰ)由题意知: ,
,
又∵PF1+PF2=4,
∴动点P(x,y)必在以F1,F2为焦点,长轴长为4的椭圆,∴a=2,
又∵ ,b2=a2-c2=1.
,b2=a2-c2=1.
∴椭圆C的方程为 .
.
(Ⅱ)由题意,可设直线l为:x=my+1.
取m=0,得 ,直线A1R的方程是
,直线A1R的方程是 ,5
,5
直线A2Q的方程是 ,交点为
,交点为 .
.
若 ,由对称性可知交点为
,由对称性可知交点为 .
.
若点S在同一条直线上,则直线只能为?:x=4.
以下证明对于任意的m,直线A1R与直线A2Q的交点S均在直线?:x=4上.
事实上,由 ,得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,
,得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,
记R(x1,y1),Q(x2,y2),则 .
.
设A1R与?交于点S(4,y),由 ,得
,得 .
.
设A2Q与?交于点S′(4,y′),由 ,得
,得 .
.
∵
=
=
= ,
,
∴y=y′,即S与S′重合,
这说明,当m变化时,点S恒在定直线?:x=4上.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 -y2=1,则|FF2|=2
-y2=1,则|FF2|=2  ,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.(II)对于存在性问题,可先假设存在,假设存在满足条件的直线l在变化时,点S是否恒在一条定直线上,设直线a的方程为x=my+1,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用条件即可求得直线的方程,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(Ⅰ)由题意知:
 ,
,又∵PF1+PF2=4,
∴动点P(x,y)必在以F1,F2为焦点,长轴长为4的椭圆,∴a=2,
又∵
 ,b2=a2-c2=1.
,b2=a2-c2=1.∴椭圆C的方程为
 .
.(Ⅱ)由题意,可设直线l为:x=my+1.
取m=0,得
 ,直线A1R的方程是
,直线A1R的方程是 ,5
,5直线A2Q的方程是
 ,交点为
,交点为 .
.若
 ,由对称性可知交点为
,由对称性可知交点为 .
.若点S在同一条直线上,则直线只能为?:x=4.
以下证明对于任意的m,直线A1R与直线A2Q的交点S均在直线?:x=4上.
事实上,由
 ,得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,
,得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,记R(x1,y1),Q(x2,y2),则
 .
.设A1R与?交于点S(4,y),由
 ,得
,得 .
.设A2Q与?交于点S′(4,y′),由
 ,得
,得 .
.∵

=

=

=
 ,
,∴y=y′,即S与S′重合,
这说明,当m变化时,点S恒在定直线?:x=4上.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 的两焦点为F、F',若该双曲线与抛物线y2=8x有一个公共的焦点F,且两曲线的一个
的两焦点为F、F',若该双曲线与抛物线y2=8x有一个公共的焦点F,且两曲线的一个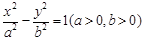 的两焦点为
的两焦点为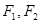 ,过
,过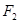 作
作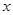 轴的垂线交双曲线于
轴的垂线交双曲线于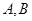 两点,若
两点,若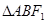 内切圆的半径为
内切圆的半径为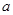 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )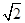 B.
B.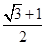 C.
C.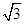 D.
D.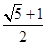
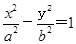 的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是
的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是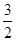 ]
B.(1,
]
B.(1,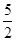 ] D.(
] D.(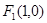 ,
,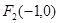 ,直线
,直线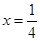 是双曲线的一条准线,
是双曲线的一条准线,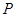 在双曲线右支上,且
在双曲线右支上,且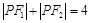 ,求
,求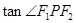 的值。
的值。