题目内容
设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2 011)+f(2 012)=
| A.3 | B.2 | C.1 | D.0 |
A
解析试题分析: .
.
考点:本小题考查了函数的周期性及函数的图像等知识.
点评:利用周期性把要求的变量的函数值转化到已给的区间(-2,1]内的变量的函数值.通常还要借助函数的奇偶性.

练习册系列答案
相关题目
下列各组函数中,f(x)与g(x)表示同一函数的是( )
A.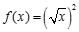 与 与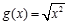 | B.f(x)=x与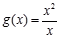 |
C.f(x)=x与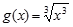 | D.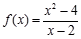 与g(x)=x+2 与g(x)=x+2 |
函数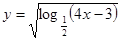 的定义域为 ( )
的定义域为 ( )
A.(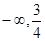 ) ) | B.(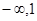 ] ] | C.(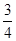 ,1] ,1] | D.(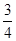 ,1) ,1) |
设集合 ,
, 则
则 ( )
( )
A. | B. | C. | D. |
偶函数 在区间
在区间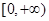 单调增加,则满足
单调增加,则满足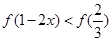 的
的 取值范围是( )
取值范围是( )
A.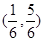 | B.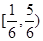 | C.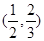 | D. |
设函数 ,则
,则 ( )
( )
A.在区间 内均有零点 内均有零点 |
B.在区间 内均无零点 内均无零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |
如果两个函数的对应关系相同,值域相同,但定义域不同,则这两个函数为“同族函数”,那么函数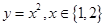 的“同族函数”有( )
的“同族函数”有( )
| A.3个 | B.7个 | C.8个 | D.9个 |
函数 的值域是
的值域是
A. | B. | C. | D. |
已知函数 的定义域为
的定义域为 ,
, 是偶函数,且
是偶函数,且 在
在 上是增函数,则
上是增函数,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |