题目内容
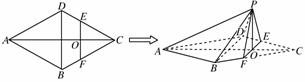
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=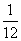 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.
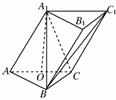
解析: (1)证明:∵AA1=A1C=AC=2,且O为AC中点,
∴A1O⊥AC,又∵侧面AA1C1C⊥底面ABC,侧面AA1C1C∩底面ABC=AC,A1O⊂平面A1AC,
∴A1O⊥平面ABC.
(2)∵VE-BCC1=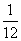 VABC-A1B1C1=
VABC-A1B1C1=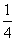 VA1-BCC1,∴BE=
VA1-BCC1,∴BE=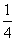 BA1,即A1E=
BA1,即A1E=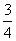 A1B.
A1B.
连接OB,在Rt△A1OB中,A1O⊥OB,A1O=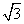 ,BO=1,故A1B=2,则A1E的长度为
,BO=1,故A1B=2,则A1E的长度为 .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程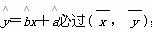 ;
;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1
C.2 D.3
本题可以参考独立性检验临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 =3e1+2e2,
=3e1+2e2, =2e1-5e2,
=2e1-5e2, =λe1-e2.若三点A、B、D共线,则λ=________.
=λe1-e2.若三点A、B、D共线,则λ=________.

 ,则tan
,则tan =( )
=( )
 D.-7
D.-7 +
+ +
+ 的最大值.
的最大值.