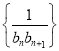题目内容
【题目】设命题![]() :
: ![]() ,函数
,函数![]() 有意义;命题
有意义;命题![]() :
: ![]() ,不等式
,不等式![]() 恒成立,如果命题“
恒成立,如果命题“![]() 或
或![]() ”为真命题,命题“
”为真命题,命题“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:分别求出命题p,q为真命题时的等价条件,利用命题p或q为真命题,p且q为假命题,所以命题![]() 与
与![]() 中一个是真命题,一个是假命题,求a的范围即可.
中一个是真命题,一个是假命题,求a的范围即可.
试题解析:
若命题![]() 为真命题,则
为真命题,则![]() 对任意
对任意![]() 均成立,
均成立,
当![]() 时,显然不符合题意,
时,显然不符合题意,
故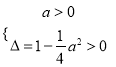 ,解得
,解得![]()
所以命题![]() 为真
为真![]()
若命题![]() 为真命题,则不等式
为真命题,则不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
即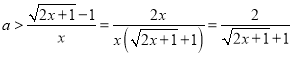 对任意
对任意![]() 恒成立
恒成立
而函数![]() 在
在![]() 为减函数,
为减函数,
所以![]() ,即
,即![]()
所以命题![]() 为真
为真![]()
因为命题“![]() 或
或![]() ”为真命题,命题“
”为真命题,命题“![]() 且
且![]() ”为假命题,
”为假命题,
所以命题![]() 与
与![]() 中一个是真命题,一个是假命题,
中一个是真命题,一个是假命题,
当![]() 为真命题,
为真命题, ![]() 为假命题时,
为假命题时, ![]() 的值不存在;
的值不存在;
当![]() 为真命题,
为真命题, ![]() 为假命题时,
为假命题时, ![]()
综上知,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目