题目内容
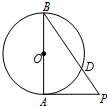（2013•北京）如图，AB为圆O的直径，PA为圆O的切线，PB与圆O相交于D，若PA=3，PD：DB=9：16，则PD=| 9 |
| 5 |
| 9 |
| 5 |
4
4
．分析：由PD：DB=9：16，可设PD=9x，DB=16x．利用切割线定理可得PA2=PD•PB，即可求出x，进而得到PD，PB．AB为圆O的直径，PA为圆O的切线，利用切线的性质可得AB⊥PA．再利用勾股定理即可得出AB．
解答：解：由PD：DB=9：16，可设PD=9x，DB=16x．
∵PA为圆O的切线，∴PA2=PD•PB，
∴32=9x•（9x+16x），化为x2=
，∴x=
．
∴PD=9x=
，PB=25x=5．
∵AB为圆O的直径，PA为圆O的切线，∴AB⊥PA．
∴AB=
=
=4．
故答案分别为
，4．
∵PA为圆O的切线，∴PA2=PD•PB，
∴32=9x•（9x+16x），化为x2=
| 1 |
| 25 |
| 1 |
| 5 |
∴PD=9x=
| 9 |
| 5 |
∵AB为圆O的直径，PA为圆O的切线，∴AB⊥PA．
∴AB=
| PB2-PA2 |
| 52-32 |
故答案分别为
| 9 |
| 5 |
点评：熟练掌握圆的切线的性质、切割线定理、勾股定理是解题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
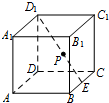（2013•北京）如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为
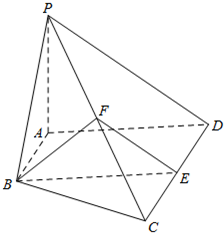（2013•北京）如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E和F分别是CD和PC的中点，求证：
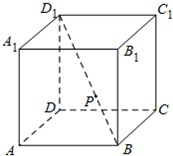（2013•北京）如图，在正方体ABCD-A1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有（ ）
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．