题目内容
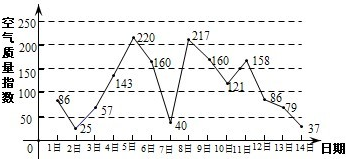
 (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1上存在点D,使得AD⊥A1B,并求
| BD | BC1 |
分析:(I)利用AA1C1C是正方形,可得AA1⊥AC,再利用面面垂直的性质即可证明;
(II)利用勾股定理的逆定理可得AB⊥AC.通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得到二面角;
(III)设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D(t,
(4-t),t),利用向量垂直于数量积得关系即可得出.
(II)利用勾股定理的逆定理可得AB⊥AC.通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得到二面角;
(III)设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D(t,
| 3 |
| 4 |
解答:(I)证明:∵AA1C1C是正方形,∴AA1⊥AC.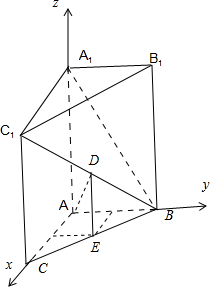
又∵平面ABC⊥平面AA1C1C,平面ABC∩平面AA1C1C=AC,
∴AA1⊥平面ABC.
(II)解:由AC=4,BC=5,AB=3.
∴AC2+AB2=BC2,∴AB⊥AC.
建立如图所示的空间直角坐标系,则A1(0,0,4),B(0,3,0),B1(0,3,4),C1(4,0,4),
∴
=(4,-3,4),
=(0,-3,4),
=(0,0,4).
设平面A1BC1的法向量为
=(x1,y1,z1),平面B1BC1的法向量为
=(x2,y2,z2).
则
,令y1=4,解得x1=0,z1=3,∴
=(0,4,3).
,令x2=3,解得y2=4,z2=0,∴
=(3,4,0).
cos<
,
>=
=
=
.
∴二面角A1-BC1-B1的余弦值为
.
(III)设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D(t,
(4-t),t),
∴
=(t,
(4-t),t),
=(0,3,-4),
∵
⊥
,∴
•
=0,
∴0+
(4-t)-4t=0,解得t=
.
∴
=
=
.

又∵平面ABC⊥平面AA1C1C,平面ABC∩平面AA1C1C=AC,
∴AA1⊥平面ABC.
(II)解:由AC=4,BC=5,AB=3.
∴AC2+AB2=BC2,∴AB⊥AC.
建立如图所示的空间直角坐标系,则A1(0,0,4),B(0,3,0),B1(0,3,4),C1(4,0,4),
∴
| BC1 |
| BA1 |
| BB1 |
设平面A1BC1的法向量为
| n1 |
| n2 |
则
|
| n1 |
|
| n2 |
cos<
| n1 |
| n2 |
| ||||
|
|
| 16 | ||||
|
| 16 |
| 25 |
∴二面角A1-BC1-B1的余弦值为
| 16 |
| 25 |
(III)设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D(t,
| 3 |
| 4 |
∴
| AD |
| 3 |
| 4 |
| A1B |
∵
| AD |
| A1B |
| AD |
| A1B |
∴0+
| 9 |
| 4 |
| 36 |
| 25 |
∴
| BD |
| BC1 |
| DE |
| CC1 |
| 9 |
| 25 |
点评:本题综合考查了线面垂直的判定与性质定理、面面垂直的性质定理、通过建立空间直角坐标系利用法向量求二面角的方法、向量垂直与数量积得关系等基础知识与基本方法,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2013•北京)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为
(2013•北京)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为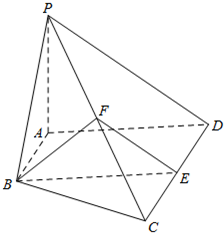 (2013•北京)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证:
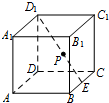
(2013•北京)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证: (2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
(2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )