题目内容

5．a、b、c、d、e是从集合{1，2，3，4，5}中任取的5个元素（不允许重复），则abc+de为奇数的概率为（　　）
A．$\frac{4}{15}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{1}{2}$

分析 先根据分类计数原理求出abc+de为奇数的种数，再求出所有的种数，根据概率公式计算即可．

解答 解：分两类讨论：
①abc为奇数，de为偶数，
此时，a，b，c必定都为奇数，故有A33A22=12种，
②abc为偶数，de为奇数，
此时，d，e必定为奇数，故有A32A33=36种，
根据分类计数原理可得，abc+de为奇数的种数为：48种，
而所有的种数为A55=120，
故abc+de为奇数的概率为$\frac{48}{120}$=$\frac{2}{5}$，
故选：B．

点评 本题考查了分类计数原理和概率公式的问题，关键是分类，属于中档题．

练习册系列答案
相关题目
15．已知正项数列{an}的前n项和为Sn，且满足Sn=2an-$\frac{1}{2}$．
（1）证明；数列{an}是等比数列；
（2）设bn=log2a2n+1，求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn．
16．在△ABC中，设$\overrightarrow{CB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$且|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}•\overrightarrow{b}$=-$\sqrt{3}$，求AB．
13．若a＞b．则下列各式正确的是（　　）
A．a•lgx＞b•lgxB．ax2＞bx2C．a2＞b2D．a•2x＞b•2x
20．已知数列{an}的首项a1=$\frac{3}{5}$，且an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$，n∈N•．
（1）求证：数列{$\frac{1}{{a}_{n}}$-1}是等比数列：
（2）令bn=$\frac{1}{{a}_{n}}$-1，试求数列{n•bn}的前n项和Sn．
10．已知$\frac{3π}{2}$＜α＜2π，且cosα=$\frac{1}{4}$，求$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}}$的值．
17．已知a＞b＞c，且a+b+c=0，则下列不等式中正确的是（　　）
A．a2＞b2＞c2B．ac＞bcC．ab＞acD．a|b|＞c|b|
14．已知二次函数f（x）=ax2+bx-3在x=1处取得极值，且在（0，-3）点处的切线与直线2x+y=0平行．
（1）求f（x）的解析式；
（2）求函数g（x）=xf（x）+4x在x∈[0，2]的最值．
4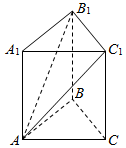．如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，$A{A_1}=\sqrt{6}$，则AA1与平面AB1C1所成的角为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网