题目内容
在平面直角坐标系中,动点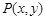 到两条坐标轴的距离之和等于它到点
到两条坐标轴的距离之和等于它到点 的距离,记点
的距离,记点 的轨迹为曲线
的轨迹为曲线 .
.
(I) 给出下列三个结论:
①曲线 关于原点对称;
关于原点对称;
②曲线 关于直线
关于直线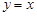 对称;
对称;
③曲线 与
与 轴非负半轴,
轴非负半轴,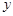 轴非负半轴围成的封闭图形的面积小于
轴非负半轴围成的封闭图形的面积小于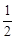 ;
;
其中,所有正确结论的序号是_____;
(Ⅱ)曲线 上的点到原点距离的最小值为______.
上的点到原点距离的最小值为______.
②③;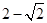
解析试题分析:(I)P点到两坐标轴距离分别为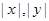 曲线
曲线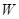 方程为
方程为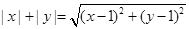 ,该方程中用
,该方程中用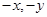 分别替换原方程中的
分别替换原方程中的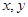 方程改变,所以曲线
方程改变,所以曲线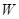 不关于原点对称;而用
不关于原点对称;而用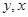 分别替换原方程中的
分别替换原方程中的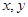 方程不变,所以曲线
方程不变,所以曲线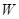 关于直线
关于直线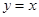 对称.曲线
对称.曲线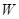 与x轴非负半轴,
与x轴非负半轴,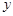 轴非负半轴围成的封闭图形即为
轴非负半轴围成的封闭图形即为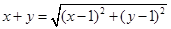 与x轴非负半轴,
与x轴非负半轴,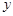 轴非负半轴围成的封闭图形,由
轴非负半轴围成的封闭图形,由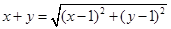 化简得:
化简得: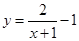 ,它的图象可由
,它的图象可由 向左平移一个单位,再向下平移1个单位而得到,它的图象与两坐标轴的交点为
向左平移一个单位,再向下平移1个单位而得到,它的图象与两坐标轴的交点为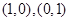 ,结合图象可知:
,结合图象可知: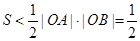 ,故正确的序号为②③.(Ⅱ)由
,故正确的序号为②③.(Ⅱ)由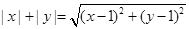 得:
得: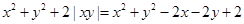 ,即
,即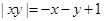 ,当
,当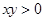 时,该式可化简为
时,该式可化简为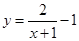 ;当
;当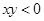 时,该式可化简为
时,该式可化简为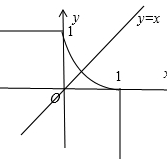
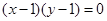 ,即
,即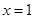 或
或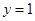 ,进而可以画出曲线
,进而可以画出曲线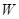 ,结合图象可知,曲线
,结合图象可知,曲线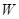 与直线
与直线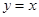 在第一象限的交点距离原点最近,由
在第一象限的交点距离原点最近,由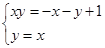 解得:
解得: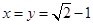 ,故最短距离为
,故最短距离为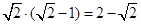 .
.
考点:曲线与方程.

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过
,过 的直线与双曲线的右支交于
的直线与双曲线的右支交于 两点,若
两点,若 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则 _______.
_______. 、
、 是双曲线
是双曲线 的焦点,点P在双曲线上,若点P到焦点
的焦点,点P在双曲线上,若点P到焦点 为椭圆
为椭圆 上一点,
上一点, 为两焦点,
为两焦点, ,则椭圆
,则椭圆 .
.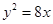 上一点
上一点 到
到 轴的距离是
轴的距离是 ,则点
,则点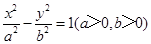 的左顶点与抛物线
的左顶点与抛物线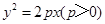 的焦点的距离为
的焦点的距离为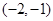 ,则双曲线的焦距为 .
,则双曲线的焦距为 . 的离心率为
的离心率为 , 则m等于 .
, 则m等于 .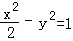 ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“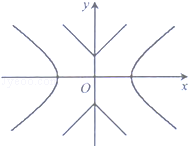
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”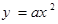
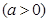 过点(4,2),则抛物线C的焦点坐标为 .
过点(4,2),则抛物线C的焦点坐标为 .