题目内容
 空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是________.
空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是________.
(8,10)
分析:本体可以设出参变量(比例),利用有关比例性质建立函数关系可解答,即设 =
= =k,则有
=k,则有 =
=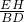 =1-k,在根据k的范围0<k<1(当点H与重合时k=0但取不到0,当H与A重合时k=1,但取不到1),从而可得结果.
=1-k,在根据k的范围0<k<1(当点H与重合时k=0但取不到0,当H与A重合时k=1,但取不到1),从而可得结果.
解答:如图所示,设 =
= =k,∴
=k,∴ =
=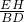 =1-k,
=1-k,
∴GH=5k,EH=4(1-k),∴周长=8+2k.
又∵0<k<1,∴周长的范围为(8,10).
故答案为:(8,10)
点评:本题考查空间四边形的概念,平面的性质,对空间几何结构的认知与把握,具体解答中用到了平行线分线段成比例的性质.
分析:本体可以设出参变量(比例),利用有关比例性质建立函数关系可解答,即设
 =
= =k,则有
=k,则有 =
=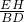 =1-k,在根据k的范围0<k<1(当点H与重合时k=0但取不到0,当H与A重合时k=1,但取不到1),从而可得结果.
=1-k,在根据k的范围0<k<1(当点H与重合时k=0但取不到0,当H与A重合时k=1,但取不到1),从而可得结果.解答:如图所示,设
 =
= =k,∴
=k,∴ =
=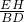 =1-k,
=1-k,∴GH=5k,EH=4(1-k),∴周长=8+2k.
又∵0<k<1,∴周长的范围为(8,10).
故答案为:(8,10)
点评:本题考查空间四边形的概念,平面的性质,对空间几何结构的认知与把握,具体解答中用到了平行线分线段成比例的性质.

练习册系列答案
相关题目
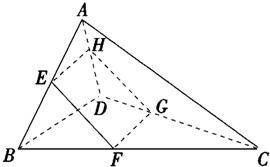 空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是
空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是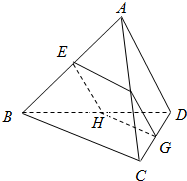 空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.
空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.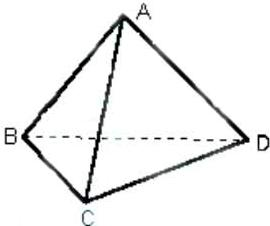 如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.
如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.