题目内容
已知点M与两个定点E(8,0),F(5,0)的距离之比等于2,设点M的轨迹为C.(Ⅰ)求曲线C的方程;
(Ⅱ)若直线l:y=kx与曲线C相交于不同的两点A、B.
(1)求k的取值范围;
(2)分别取k=0及k=
| 1 |
| 2 |
| |AQ| |
| |QB| |
| |OA| |
| |OB| |
分析:(I)设出动点M的坐标,然后根据点M与两个定点E(8,0),F(5,0)的距离之比等于2,利用两点之间的距离公式,整理后,即可得到曲线C的方程;
(II)(1)结合(I)的结论,直线l:y=kx与曲线C相交于不同的两点A、B,则直线与圆相交,则圆心到直线的距离小于半径,由此构造关于k的方程,即可得到答案.
(2)将k=0及k=
代入,求出满足条件的Q的坐标,分析后可猜想Q在直线x=3上.则我们可以联立方程,求出满足条件的直线方程,验证是否为直线x=3;
(II)(1)结合(I)的结论,直线l:y=kx与曲线C相交于不同的两点A、B,则直线与圆相交,则圆心到直线的距离小于半径,由此构造关于k的方程,即可得到答案.
(2)将k=0及k=
| 1 |
| 2 |
解答:解:(Ⅰ)设M(x,y),依题意有:
=2,
∴
=2,(2分)
整理得曲线C的方程为(x-4)2+y2=4.(4分)
解:(Ⅱ)(1)由(Ⅰ)知,要使线l:y=kx与曲线C相交于不同的两点,只需曲线C的圆心(4,0)到直线l的距离小于圆的半径2.
∴
<2,
解得,-
<k<
.(7分)
(2)设A(x1,y1),B(x2,y2),Q(x0,y0),则有0<x1<x0<x2.
当k=0时,A(2,0),B(6,0),
由
=
知,
=
,
∴x0=3,即点Q的坐标为(3,0).(8分)
当k=
时,由
得方程5x2-32x+48=0,∴x1+x2=
,x1x2=
由
=
知,
=
,
整理得x0=
=3,∴y0=
∴即点Q的坐标为(3,
).(10分)
猜想,点Q在直线x=3上.(11分)
证明如下:
方法1,由
得(1+k2)x2-8x+12=0,(12分)
∴x1+x2=
①,x1x2=
②
由
=
知,
=
,
整理得x0=
=3
即点Q在定直线上,这条直线的方程是x=3.(15分)
| |ME| |
| |MF| |
∴
| ||
|
整理得曲线C的方程为(x-4)2+y2=4.(4分)
解:(Ⅱ)(1)由(Ⅰ)知,要使线l:y=kx与曲线C相交于不同的两点,只需曲线C的圆心(4,0)到直线l的距离小于圆的半径2.
∴
| |4k| | ||
|
解得,-
| ||
| 3 |
| ||
| 3 |
(2)设A(x1,y1),B(x2,y2),Q(x0,y0),则有0<x1<x0<x2.
当k=0时,A(2,0),B(6,0),
由
| |AQ| |
| |QB| |
| |OA| |
| |OB| |
| x0-2 |
| 6-x0 |
| 2 |
| 6 |
∴x0=3,即点Q的坐标为(3,0).(8分)
当k=
| 1 |
| 2 |
|
得方程5x2-32x+48=0,∴x1+x2=
| 32 |
| 5 |
| 48 |
| 5 |
由
| |AQ| |
| |QB| |
| |OA| |
| |OB| |
| x0-x1 |
| x2-x0 |
| x1 |
| x2 |
整理得x0=
| 2x1x2 |
| x1+x2 |
| 3 |
| 2 |
∴即点Q的坐标为(3,
| 3 |
| 2 |
猜想,点Q在直线x=3上.(11分)
证明如下:
方法1,由
|
得(1+k2)x2-8x+12=0,(12分)
∴x1+x2=
| 8 |
| 1+k2 |
| 12 |
| 1+k2 |
由
| |AQ| |
| |QB| |
| |OA| |
| |OB| |
| x0-x1 |
| x2-x0 |
| x1 |
| x2 |
整理得x0=
| 2x1x2 |
| x1+x2 |
即点Q在定直线上,这条直线的方程是x=3.(15分)
点评:本题考查的知识点是直线与圆的位置关系,其中利用坐标法求了满足条件的动点M的轨迹C是解答本题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 ,在弦AB上,确定点Q的坐标,使
,在弦AB上,确定点Q的坐标,使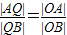 (|OA|<|OB|)成立.由此猜想出一般结论,并给出证明.
(|OA|<|OB|)成立.由此猜想出一般结论,并给出证明. ,在弦AB上,确定点Q的坐标,使
,在弦AB上,确定点Q的坐标,使 (|OA|<|OB|)成立.由此猜想出一般结论,并给出证明.
(|OA|<|OB|)成立.由此猜想出一般结论,并给出证明.