题目内容
过点P(-1,0)作圆C:(x - 1)2 + (y - 2)2 = 1的两切线,设两切点为A、B,圆心为C,则过A、B、C的圆方程是
A.x2 + (y - 1)2 = 2 B.x2 + (y - 1)2 = 1
C.(x - 1)2 + y2 = 4 D.(x - 1)2 + y2 = 1
A
解析:
因为C(1,2),线段PC的中点M(0,1)就是所求圆的圆心,半径为![]() ,所以过A、B、C的圆方程是
,所以过A、B、C的圆方程是![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
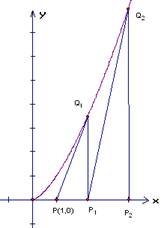
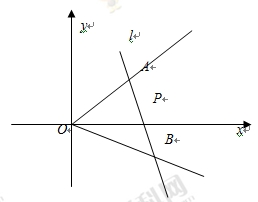
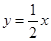 上时,求直线AB的方程.
上时,求直线AB的方程.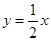 上时,求直线AB的方程.
上时,求直线AB的方程.