题目内容
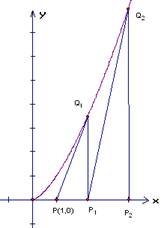
(08年咸阳市一模) (14分)如图,过点P(1,0)作曲线C: ![]() 的切线,切点为
的切线,切点为![]() ,设
,设![]() 点在x轴上的投影是点
点在x轴上的投影是点![]() ;又过点
;又过点![]() 作曲线C的切线,切点为
作曲线C的切线,切点为![]() ,设
,设![]() 在x轴上的投影是
在x轴上的投影是![]() ;…;依此下去,得到一系列点
;…;依此下去,得到一系列点![]() ,
,![]() ,…,
,…,![]() ,…,设点
,…,设点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)试求数列{![]() }的通项公式
}的通项公式![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(Ⅱ)求证:![]()
(Ⅲ)求证:![]() (注:
(注:![]() ).
).
解析: (Ⅰ) ![]()
![]() ,若切点是
,若切点是![]() ,则
,则
切线方程为![]() . 1分
. 1分
当n=1时,切线过点(1,0),即![]() ,得
,得![]()
当n>1时,切线过点![]() ,即
,即![]() ,解得
,解得![]() .
.
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
故所求通项![]() . 4分
. 4分
(Ⅱ) 由(1)知![]()
![]()
![]()
![]() 9分
9分
(Ⅲ)设![]() ,则
,则![]() ,
,
两式相减得![]() ,
,
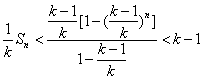 . 故
. 故
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目