题目内容
已知
(1)求 的最小值及取最小值时
的最小值及取最小值时 的值。
的值。
(2)若 ,求
,求 的取值范围。
的取值范围。
(1) ,
, ;(2)
;(2) 。
。
解析试题分析:(1)根据柯西不等式的一般形式可得 ,把已知条件可化为
,把已知条件可化为 ,即可求出
,即可求出 的最小值,注意等号成立的条件;(2)由柯西不等式得到不等式,再利用等量代换转化为关于
的最小值,注意等号成立的条件;(2)由柯西不等式得到不等式,再利用等量代换转化为关于 的不等式求解。
的不等式求解。
试题解析:(1)根据柯西不等式得: 、

 ,
,
即 ,∴
,∴ ,等号成立的条件是
,等号成立的条件是 ,
,
∴当 时,
时, 。
。
(2)根据条件可得 ,根据柯西不等式得:
,根据柯西不等式得:
即 ,∴
,∴ ,解之得
,解之得 。
。
考点:利用柯西不等式求最值或求参数的范围。

练习册系列答案
相关题目
 的最大值为 .
的最大值为 .
 ;
;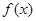 的最小值.
的最小值. (2)
(2)
 ,且
,且 .
. 的最小值
的最小值 ;
; 满足
满足 ,求证:
,求证: .
.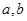 满足
满足 ,证明:
,证明: .
. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。 ≥2y+3.
≥2y+3.