题目内容
边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C-ABD，它的主视图与俯视图如图所示，则异面直线AB与CD所成角为60°
60°
．分析：设折叠前C点的位置为C'，AC、BD的交点为O．因为AB∥C'D，所以∠CDC'（或其补角）就是异面直线AB与CD的所成角．再根据三视图，证出CO⊥平面ABD，在Rt△OCC'中求出CC'=1进而得到△DCC'是等边三角形，由此即得∠CDC'=60°，可得面直线AB与CD所成角．
解答：解：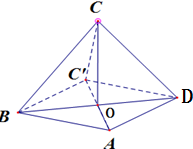
设折叠前C点的位置为C'，AC、BD的交点为O，则
∵根据三视图，可得平面BCD⊥平面ABD，平面BCD∩平面ABD=BD且CO⊥BD
∴CO⊥平面ABD
∵OC'?平面ABD，∴CO⊥OC'
∵CO=C'O=
，∴CC'=
=1
∵DC'=DC=1，∴△DCC'是边长为1的等边三角形，可得∠CDC'=60°
∵正方形ABC'D中，AB∥C'D，
∴∠CDC'就是异面直线AB与CD的所成角，
因此，异面直线AB与CD的所成角为60°
故答案为：60°
设折叠前C点的位置为C'，AC、BD的交点为O，则∵根据三视图，可得平面BCD⊥平面ABD，平面BCD∩平面ABD=BD且CO⊥BD
∴CO⊥平面ABD
∵OC'?平面ABD，∴CO⊥OC'
∵CO=C'O=
| ||
| 2 |
| OC2+C′O2 |
∵DC'=DC=1，∴△DCC'是边长为1的等边三角形，可得∠CDC'=60°
∵正方形ABC'D中，AB∥C'D，
∴∠CDC'就是异面直线AB与CD的所成角，
因此，异面直线AB与CD的所成角为60°
故答案为：60°
点评：本题以平面图形的翻折为例，在给出三棱锥的三视图的情况下求异面直线所成角．着重考查了面面垂直的性质、三视图的认识和异面直线所成角的求法等知识，属于基础题．
练习册系列答案
相关题目
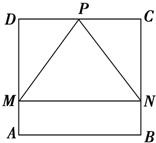如图，四边形ABCD是一个边长为1的正方形，△MPN是正方形的一个内接正三角形，且MN∥AB，若向正方形内部随机投入一个质点，则质点恰好落在△MPN的概率为（ ）
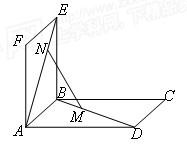如图，两个边长为1的正方形ABCD与ABEF相交于AB，∠EBC=90°，M，N分别是BD，AE上的点，且AN=DM．
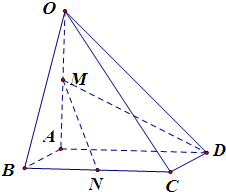如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC中点，以A为原点，建立适当的空间直角坐标系，利用空间向量解答以下问题
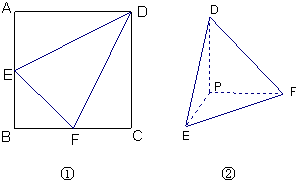（2011•揭阳一模）如图①边长为1的正方形ABCD中，点E、F分别为AB、BC的中点，将△BEF剪去，将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点P得一三棱锥如图②示．