题目内容
（本题满分20分）
设
是定义在实数
上的函数，
是定义在正整数
上的函数，同时满足下列条件：
（1）任意
，有
，当
时，
且
；
（2）
；
（3）
，
试求：（1）证明：任意， 
，都有
；
（2）是否存在正整数
，使得
是25的倍数，若存在，求出所有自然数；若不存在说明理由． （阶乘定义：
）
【答案】
【解析】解：（1）当
时，
， 
，
若
，则得
，不可能，舍去 
当
时，
，得，
若
，则，
，
，
，
同理，若
，
任意
，
，都有
（2）
由（1）可得
为单调减函数
得
…
相乘得：
…①
又由①式得：
…
，
相加得：
，
，
，
，
，
，
，
，
，
由于当
时，
能被25整除
综上，存在正整数
，当
或
时，
是25的倍数
练习册系列答案
相关题目
是直线
上的
个不同的点（
，
、
均为非零常数），其中数列
为等差数列.
是等差数列；
是直线
上一点，且
，求证: 
；
，且当
时，恒有
（
和
都是不大于
）.试探索：在直线
成立？请说明你的理由.
中，已知
，…，
是直线
上的
个点（
，
、
均为非零常数）.
成等差数列，求证：数列
也成等差数列；
是直线
上一点，且
，求
的值；
，我们称
是向量
，
，…，
的线性组合,
是该线性组合的系数数列.
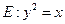
与圆
相交于A、B、C、D四个点。