题目内容
设F1，F2分别是椭圆：
+
=1(a＞b＞0)的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|=
a．
（Ⅰ）求该椭圆的离心率；
（Ⅱ）设点M（0，-1）满足|MP|=|MQ|，求该椭圆的方程．
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
（Ⅰ）求该椭圆的离心率；
（Ⅱ）设点M（0，-1）满足|MP|=|MQ|，求该椭圆的方程．
分析：（1）设直线l的方程为y=x+c，与椭圆方程消去y得关于x的一元二次方程，利用根与系数的关系，得P、Q横坐标之和与横坐标之积关于a、b、c的式子．再用弦长公式结合PQ的长度为
，列出关于a、b、c的方程，化简整理可得a=
b，由此不难求出该椭圆的离心率．
（2）根据|MP|=|MQ|，得M点在PQ的中垂线上，由此结合（1）中的条件，列出关于c的方程并解之得c=3，再根据离心率算出a、b之值，即可得到该椭圆的方程．
| 4a |
| 3 |
| 2 |
（2）根据|MP|=|MQ|，得M点在PQ的中垂线上，由此结合（1）中的条件，列出关于c的方程并解之得c=3，再根据离心率算出a、b之值，即可得到该椭圆的方程．
解答：解：（Ⅰ）由直线PQ斜率为1，可设直线l的方程为y=x+c，其中c=
．…（2分）
设P（x1，y1），Q（x2，y2），则两点坐标满足方程组
消去y，整理得（a2+b2）x2+2a2cx+a2（c2-b2）=0，
可得：
∵|PQ|=
a，∴
|x1-x2|=
a
由此可得|x1-x2|2=(x1+x2)2-4x1x2=(
a)2
即（
）2-4（
）2=
．…（6分）
整理，得a2=2b2，a=
b
∴椭圆的离心率e=
=
=
．…（8分）
（Ⅱ）设PQ 中点为N（x0，y0），由（1）知
x0=
=
=-
，y0=x0+c=
c．
由|MP|=|MQ|，得MN与直线y=x+c垂直，所以MN的斜率k=-1．…（10分）
∴
=-1，即
=-1，解得c=3，从而a=3
，b=3．
因此，椭圆的方程为
+
=1…（12分）
| a2-b2 |
设P（x1，y1），Q（x2，y2），则两点坐标满足方程组
|
消去y，整理得（a2+b2）x2+2a2cx+a2（c2-b2）=0，
可得：
|
∵|PQ|=
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
由此可得|x1-x2|2=(x1+x2)2-4x1x2=(
2
| ||
| 3 |
即（
| -2a2c |
| a 2+b2 |
| a2(c2-b2) |
| a 2+b2 |
| 8a2 |
| 9 |
整理，得a2=2b2，a=
| 2 |
∴椭圆的离心率e=
| c |
| a |
|
| ||
| 2 |
（Ⅱ）设PQ 中点为N（x0，y0），由（1）知
x0=
| x1+x2 |
| 2 |
| -a2c |
| a 2+b2 |
| 2c |
| 3 |
| 1 |
| 3 |
由|MP|=|MQ|，得MN与直线y=x+c垂直，所以MN的斜率k=-1．…（10分）
∴
| y0+1 |
| x0 |
| ||
-
|
| 2 |
因此，椭圆的方程为
| x2 |
| 18 |
| y2 |
| 9 |
点评：本题给出直线与椭圆相交，在已知弦长的情况下求椭圆的离心率．着重考查了椭圆的基本概念、简单几何性质和直线与椭圆的位置关系等知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
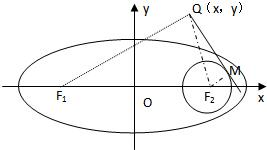设F1，F2分别是椭圆C：