题目内容
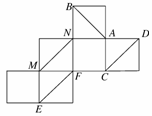
一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:
①AB⊥EF ②AB与CM成60° ③EF与MN是异面直线 ④MN∥CD
其中正确的是 ( )
A.①② B.③④ C.②③ D.①③
D

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
题目内容
一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:
①AB⊥EF ②AB与CM成60° ③EF与MN是异面直线 ④MN∥CD
其中正确的是 ( )

A.①② B.③④ C.②③ D.①③
D

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案