题目内容
已知圆C：x2＋y2＋x－6y＋m＝0与直线l：x＋2y－3＝0.
(1)若直线l与圆C没有公共点，求m的取值范围；
(2)若直线l与圆C相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．
(1)将圆的方程配方，
得(x＋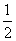
)2＋(y－3)2＝
，
故有>0，解得m<
.
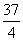将直线l的方程与圆C的方程组成方程组，得
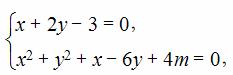
消去y，得x2＋(
)2＋x－6×＋m＝0，
整理，得5x2＋10x＋4m－27＝0，①
∵直线l与圆C没有公共点，∴方程①无解，
∴Δ＝102－4×5(4m－27)<0，解得m>8.
∴m的取值范围是(8，)．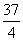
(2)设P(x1，y1)，Q(x2，y2)，
由OP⊥OQ，得
＝0，
由x1x2＋y1y2＝0，②
由(1)及根与系数的关系得，
x1＋x2＝－2，x1·x2＝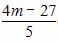
③
又∵P、Q在直线x＋2y－3＝0上，
∴y1·y2＝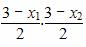
＝
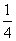[9－3(x1＋x2)＋x1·x2]，
将③代入上式，得y1·y2＝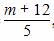
，④
将③④代入②得x1·x2＋y1·y2
＝
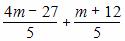＝0，解得m＝3，
代入方程①检验得Δ>0成立，∴m＝3.
练习册系列答案
阅读快车系列答案
相关题目
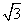B．2
B.
D.
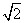，0)引直线l与曲线y＝
相交于A、B两点，O为坐标原点，当△AOB的面积取最大值时，直线l的斜率等于( )
B．－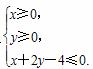
表示的平面区域恰好被面积最小的圆C：(x－a)2＋(y－b)2＝r2及其内部所覆盖，则圆C的方程为( )
＋
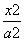＝1(a>b>0)的离心率e＝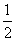
，右焦点为F(c,0)，方程ax2＋2bx＋c＝0的两个实数根分别是x1和x2，则点P(x1，x2)到原点的距离为( )
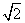B.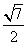
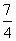
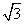y＝4相切．