题目内容
如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于B1、C1.将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M.求: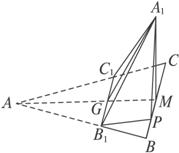
(1)二面角A1B1C1M的大小;
(2)异面直线A1B1与CC1所成角的大小(用反三角函数表示).
解析:(1)连结AM、A1G.
∵G是正三角形ABC的中心,且M为BC的中点,
∴A、G、M三点共线,AM⊥BC.
∵B1C1∥BC,∴B1C1⊥AM于G,
即GM⊥B1C1,GA1⊥B1C1.
∴∠A1GM是二面角A1-B1C1-M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,即∠A1MG=90°.
在Rt△A1GM中,由A1G=AG=2GM得∠A1GM=60°,
即二面角A1B1C1M的大小是60°.
(2)过B1作C1C的平行线交BC于P,则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得
B1P=C1C=1=BP,
PM=BM-BP=![]() ,A1B1=AB1=2.
,A1B1=AB1=2.
∵A1M⊥面BB1C1C于M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1Gsin60°=![]() .
.
在Rt△A1MP中,A1P2=A1M2+PM2=![]() .
.
在△A1B1P中,由余弦定理得cos∠A1B1P=![]() ,
,
∴异面直线A1B1与CC1所成角的大小为arccos![]() .
.
小结:求二面角、异面直线所成的角一般是先作出二面角的平面角、异面直线所成的角(平面角),然后通过解三角形可得要求的角.

练习册系列答案
相关题目
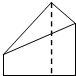
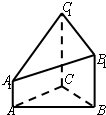 如图,△ABC为正三角形,AA1∥BB1∥CC1,CC1⊥平面ABC,且3AA1=
如图,△ABC为正三角形,AA1∥BB1∥CC1,CC1⊥平面ABC,且3AA1=
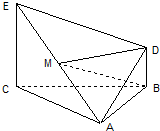 如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点. 如图,△ABC为正三角形,且直线BC的倾斜角是45°,则直线AB,AC的倾斜角分别为:αAB=
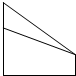
如图,△ABC为正三角形,且直线BC的倾斜角是45°,则直线AB,AC的倾斜角分别为:αAB=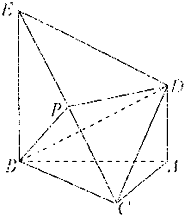 如图,△ABC为正三角形,EB⊥平面ABC,AD∥BE,且BE=AB=2AD,P是EC的中点.
如图,△ABC为正三角形,EB⊥平面ABC,AD∥BE,且BE=AB=2AD,P是EC的中点.