题目内容
16.函数f(x)=x3+x-8的零点所在的区间是( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 利用函数零点存在定理,对区间端点函数值进行符号判断,异号的就是函数零点存在的区间.
解答 解:因为f(1)=1+1-8=-6<0,
f(2)=8+2-8=2>0,
所以f(1)f(2)<0,
所以函数f(x)=x3+x-8的零点所在区间是(1,2);
故选:B.
点评 本题考查了函数零点的存在区间的判断;根据函数零点的判定定理,只要区间端点的函数值异号,就是函数零点存在区间.

练习册系列答案
相关题目
11.在△ABC中,角A,B,C所对的边分别为a,b,c.若角A,B,C成等差数列,边a,b,c成等比数列,则sinA•sinC的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
6.已知复数z=1-i,则$\frac{z-1}{{z}^{2}}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | $\frac{1}{2}$i |
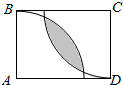 如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.
如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.