题目内容
7.已知正数x,y满足x+y-xy=0,则3x+2y的最小值为5+2$\sqrt{6}$.分析 得到$\frac{1}{x}$+$\frac{1}{y}$-=1,根据基本不等式的性质求出3x+2y的最小值即可.
解答 解:∵x+y-xy=0,
∴$\frac{1}{x}$+$\frac{1}{y}$-=1,
故3x+2y=(3x+2y)($\frac{1}{x}$+$\frac{1}{y}$)=$\frac{3x}{y}$+$\frac{2y}{x}$+5≥2$\sqrt{\frac{3x}{y}•\frac{2y}{x}}$+5=5+2$\sqrt{6}$,
当且仅当$\frac{3x}{y}$=$\frac{2y}{x}$时“=”成立,
故答案为:5+2$\sqrt{6}$.
点评 本题考查了基本不等式的性质,注意满足条件“一正二定三相等”,本题是一道基础题.

练习册系列答案
相关题目
17.在△ABC中,若2sin$\frac{B}{2}$•cos$\frac{B}{2}$•sinC=cos2$\frac{A}{2}$,则△ABC是( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 非等腰三角形 | D. | 直角三角形 |
16.为了研究某种细菌在特定环境下随时间变化的繁殖情况,得到如下实验数据:
及y关于t的线性回归方程$\hat y=0.85t-0.25$,则实验数据中m的值为3.
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | m | 4 | 4.5 | 6 |
17.方程x2-5x+1=0的两根是两圆锥曲线的离心率,它们是( )
| A. | 椭圆、双曲线 | B. | 椭圆、抛物线 | C. | 双曲线、抛物线 | D. | 无法确定 |
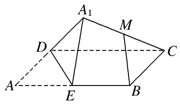 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)