题目内容
12．将函数f（x）=sin2x-cos2x的图象经过恰当平移后得到一个奇函数的图象，则这个平移可以是（ ）| A． | 向左平移$\frac{π}{8}$个单位 | B． | 向左平移$\frac{π}{4}$个单位 | ||
| C． | 向右平移$\frac{π}{8}$个单位 | D． | 向右平移$\frac{π}{4}$个单位 |
分析 由题意化简函数解析式可得f（x）=$\sqrt{2}$sin（2x-$\frac{π}{4}$），根据函数y=Asin（ωx+∅）的图象变换规律及正弦函数的性质验证选项即可得解．
解答 解：∵f（x）=sin2x-cos2x=$\sqrt{2}$sin（2x-$\frac{π}{4}$），
∴将函数f（x）的图象经过向左平移$\frac{π}{8}$个单位单位后，所得函数图象对应的函数解析式为：y=$\sqrt{2}$sin[2（x+$\frac{π}{8}$）-$\frac{π}{4}$]=$\sqrt{2}$sin2x，符合题意．
故选：A．
点评 本题主要考查三角函数的函数的奇偶性，函数y=Asin（ωx+∅）的图象变换规律，属于基础题．
练习册系列答案
相关题目
2．在空间直角坐标系中，若A（2，-2，1），B（4，2，3），C（x，y，2）三点共线，则$\left|\overrightarrow{BC}\right|$=（ ）
| A． | $\sqrt{6}$ | B． | $2\sqrt{6}$ | C． | $\sqrt{5}$ | D． | $2\sqrt{5}$ |
3．方程x5-x-1=0的一个正零点的存在区间可能是（ ）
| A． | [0，1] | B． | [1，2] | C． | [2，3] | D． | [3，4] |
20．若（1+x）4=a0+a1x+a2x2+a3x3+a4x4，则a1+a2+a3+a4的值为（ ）
| A． | 0 | B． | 15 | C． | 16 | D． | 17 |
4．
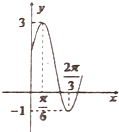如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）
如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）| A． | $y=2sin（2x+\frac{π}{6}）+1$ | B． | $y=sin（2x+\frac{π}{3}）+1$ | C． | $y=2sin（\frac{1}{2}x+\frac{π}{6}）+2$ | D． | $y=sin（2x+\frac{π}{3}）+2$ |