题目内容
满足不等式log2x+log2(3•2n-1-x)≥2n-1(n∈N*)的正整数x的个数记为an,数列{an}的前n项和记为Sn,则Sn=
- A.2n+n-1
- B.2n-1
- C.2n+1
- D.2n-n-1
A
分析:先由log2x+log2(3•2n-1-x)≥2n-1得到2n-1≤x≤2•2n-1,再求出an,根据an表达式,从而得到Sn的表达式.
解答:由log2x+log2(3•2n-1-x)≥2n-1得到2n-1
∵x是正整数∴an=2•2n-1-2n-1+1=2n-1+1,
∴Sn=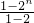 +n=2n+n-1
+n=2n+n-1
故选A.
点评:此题考查了一元二次不等式的解法与数列求和.
分析:先由log2x+log2(3•2n-1-x)≥2n-1得到2n-1≤x≤2•2n-1,再求出an,根据an表达式,从而得到Sn的表达式.
解答:由log2x+log2(3•2n-1-x)≥2n-1得到2n-1
∵x是正整数∴an=2•2n-1-2n-1+1=2n-1+1,
∴Sn=
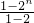 +n=2n+n-1
+n=2n+n-1 故选A.
点评:此题考查了一元二次不等式的解法与数列求和.

练习册系列答案
相关题目
满足不等式log2x+log2(3•2n-1-x)≥2n-1(n∈N*)的正整数x的个数记为an,数列{an}的前n项和记为Sn,则Sn=( )
| A、2n+n-1 | B、2n-1 | C、2n+1 | D、2n-n-1 |
 ,求Tn的最小值与最大值.
,求Tn的最小值与最大值.