题目内容
1．计算：$\underset{lim}{x→0}$$\frac{\sqrt{1+xsinx}-1}{{e}^{{x}^{2}}-1}$．分析 利用洛必达法则可得$\underset{lim}{x→0}$$\frac{\sqrt{1+xsinx}-1}{{e}^{{x}^{2}}-1}$=$\underset{lim}{x→0}$$\frac{\frac{sinx+xcosx}{2\sqrt{1+xsinx}}}{2x{e}^{{x}^{2}}}$，化简后再利用一次洛必达法则即可．
解答 解：$\underset{lim}{x→0}$$\frac{\sqrt{1+xsinx}-1}{{e}^{{x}^{2}}-1}$=$\underset{lim}{x→0}$$\frac{\frac{sinx+xcosx}{2\sqrt{1+xsinx}}}{2x{e}^{{x}^{2}}}$
=$\underset{lim}{x→0}$$\frac{sinx+xcosx}{4x}$=$\underset{lim}{x→0}$$\frac{cosx+cosx-xsinx}{4}$
=$\frac{1}{2}$．
点评 本题考查了洛必达法则的应用．
练习册系列答案
相关题目
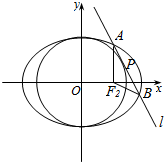已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{2}{3}$，F1、F2分别为其左、右焦点，点M为椭圆C的上的顶点，且，△MF1F2的面积为2$\sqrt{5}$．
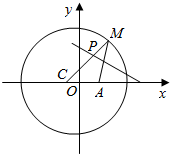已知圆C：（x+1）2+y2=25，定点A（1，0），M为圆上的一个动点，连接MA，作MA的垂直平分线交半径MC于P，当M点在圆周上运动时，点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$．
6．把45化为二进制数为（ ）
| A． | 1011112 | B． | 1011012 | C． | 1101012 | D． | 1111012 |
10．已知定义在R上的函数y=f（x）满足以下三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称
则下列结论中正确的是（ ）
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称
则下列结论中正确的是（ ）
| A． | f （4.5）＜f （7）＜f （6.5） | B． | f （7）＜f （4.5）＜f （6.5） | C． | f （7）＜f （6.5）＜f （4.5） | D． | f （4.5）＜f （6.5）＜f （7） |