Question

【题目】如图，是圆O的直径，点C是圆O上异于A，B的点，直线平面，E，F分别是，的中点.

（1）记平面与平面的交线为l，试判断直线l与平面的位置关系，并加以证明；

（2）设，求二面角大小的取值范围.

Answer 1

【答案】（1）平行，详见解析；（2）.

【解析】

（1）先证平面，再证，最后得出l平面；

（2）设直线l与圆O的另一个交点为D，连接DE，FB，易得，，可得是二面角的平面角，再由的范围得出二面角的取值范围.

（1），平面，平面，平面，

又平面，平面与平面的交线为l，所以，

而l平面，平面，所以l平面；

（2）设直线l与圆O的另一个交点为D，连接DE，FB，如图：

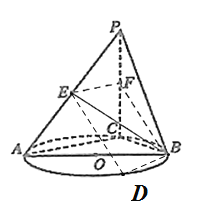
由（1）知，BDAC，而，所以，

所以平面，所以，

而，所以平面PBC，

又FB平面PBC，所以，

所以就是二面角的平面角，

因为，点F是的中点，所以，

故，

注意到，所以，所以，

因为，所以，

所以二面角大小的取值范围为.