题目内容
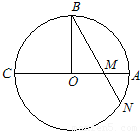 如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC=
如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC=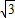 ,OM=1,则MN= .
,OM=1,则MN= .
【答案】分析:根据题设条件,先由勾股定理求出BM,再由相交弦定理求MN.
解答:解: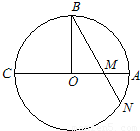 ∵AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.
∵AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.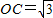 ,OM=1,
,OM=1,
∴OB=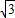 ,BM=
,BM=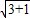 =2,
=2,
设MN=x,
∵CM•AM=BM•MN,
∴(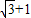 )(
)(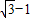 )=2x,
)=2x,
∴x=1,即MN=1.
故答案为:1.
点评:本题考查与圆有关的比例线段的应用,是基础题.解题时要认真审题,注意勾股定理和相交弦定理的灵活运用.
解答:解:
 ∵AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.
∵AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.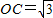 ,OM=1,
,OM=1,∴OB=
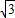 ,BM=
,BM=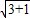 =2,
=2,设MN=x,
∵CM•AM=BM•MN,
∴(
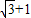 )(
)(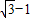 )=2x,
)=2x,∴x=1,即MN=1.
故答案为:1.
点评:本题考查与圆有关的比例线段的应用,是基础题.解题时要认真审题,注意勾股定理和相交弦定理的灵活运用.

练习册系列答案
相关题目
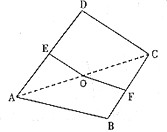 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )| A、30° | B、60° | C、120° | D、150° |
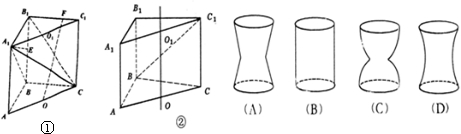
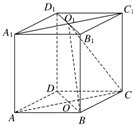 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为 (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积; 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数