题目内容
已知奇函数

(1)求实数 的值,并在给出的直角坐标系中画出
的值,并在给出的直角坐标系中画出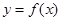 的图象;
的图象;
(2)若函数 在区间
在区间 上单调递增,试确定实数
上单调递增,试确定实数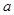 的取值范围.
的取值范围.
(1) ;(2)
;(2)  或
或
解析试题分析:(1)因为函数 式奇函数,所以
式奇函数,所以 ,取
,取 ,即可求出
,即可求出 的值,最后画出
的值,最后画出 的图像;(2)由(1)函数的图像得
的图像;(2)由(1)函数的图像得 的增区间为
的增区间为 ,又因为若函数
,又因为若函数 在区间
在区间 上单调递增,所以
上单调递增,所以

 ,得
,得

 ,即可解得
,即可解得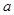 的取值范围.
的取值范围.
试题解析:(1) 函数
函数 是奇函数
是奇函数
 即
即


因此 ,所以函数
,所以函数 图像为:
图像为:
(2)从函数 图像可知
图像可知 的单调递增区间是
的单调递增区间是




因此实数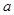 的取值范围是
的取值范围是 或
或 .
.
考点:1.函数奇偶性的性质;2.函数的解析式和图像;3.集合间的运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
 ,求它的定义域和值域。
,求它的定义域和值域。 若函数
若函数 .
. 的解析式;
的解析式; 满足
满足 ,且
,且 。
。 的奇偶性并证明之;
的奇偶性并证明之; 的不等式:
的不等式: ;
; ,
, .
. ,若集合
,若集合 有且仅有一个元素,求证:
有且仅有一个元素,求证:  。
。  ,对一切
,对一切 恒成立;命题q:函
恒成立;命题q:函 是增函数.若p或q为真,p且q为假,求实数a的取值范围.
是增函数.若p或q为真,p且q为假,求实数a的取值范围. 上的函数
上的函数 满足:①对任意
满足:①对任意 都有:
都有: ;②当
;②当
 时,
时, ,回答下列问题.
,回答下列问题. 上的单调性,并说明理由.
上的单调性,并说明理由. ,
, .
. 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数 有
有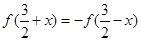 成立.
成立. 是周期函数,并指出其周期;
是周期函数,并指出其周期; ,求
,求 的值;
的值;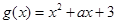 ,且
,且 是偶函数,求实数
是偶函数,求实数 的值.
的值.