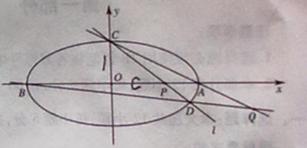题目内容
过点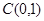 的椭圆
的椭圆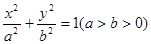 的离心率为
的离心率为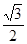 ,椭圆与
,椭圆与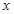 轴交于两点
轴交于两点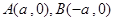 ,过点
,过点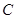 的直线
的直线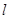 与椭圆交于另一点
与椭圆交于另一点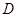 ,并与
,并与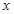 轴交于点
轴交于点 ,直线
,直线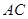 与直线
与直线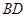 交于点
交于点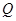
(1)当直线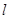 过椭圆的右焦点时,求线段
过椭圆的右焦点时,求线段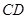 的长;
的长;
(2)当点 异于点
异于点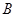 时,求证:
时,求证: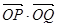 为定值
为定值
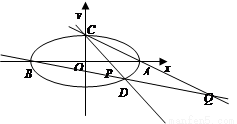
【答案】

(2)当直线 与
与 轴垂直时与题意不符,所以直线
轴垂直时与题意不符,所以直线 与
与 轴不垂直,即直线的斜率存在
轴不垂直,即直线的斜率存在
设直线 的方程为
的方程为
代入椭圆的方程,化简得 ,解得
,解得
代入直线 的方程,得
的方程,得
所以, 的坐标为
的坐标为
又直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为
联立解得 即
即
而 的坐标为
的坐标为
所以 即
即 为定值
为定值
【解析】略

练习册系列答案
相关题目
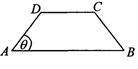
 中,
中, 且
且 ,
,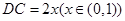 . 以
. 以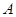 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
, ,则
,则 的取值范围为( )
的取值范围为( )
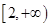 B.
B. C.
C. D.
D.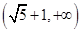
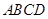 中,
中,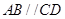 ,且
,且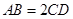 ,设
,设 ,以
,以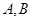 为焦点且过点
为焦点且过点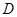 的双曲线的离心率为
的双曲线的离心率为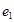 ,以
,以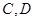 为焦点且过点
为焦点且过点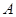 的椭圆的离心率为
的椭圆的离心率为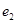 ,设
,设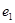 =
=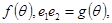 则
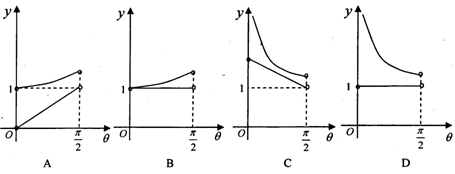
则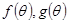 的大致图像是( )
的大致图像是( )