题目内容

19．如图，已知点A∉平面BCD，E，F，G，H分别是AB，BC，CD，DA上的点，且EH与FG交于点P．求证：P在直线BD上．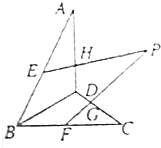

分析 由已知EH?平面ABD，FD?平面BCD，且EH∩FD=P，由此能证明P在直线BD上．

解答 解：∵点A∉平面BCD，E，F，G，H分别是AB，BC，CD，DA上的点，
∴EH?平面ABD，FD?平面BCD，
∵EH∩FD=P，
∴P∈平面ABD，且P∈平面BCD，
∵平面ABD∩平面BCD=BD，
∴P在直线BD上．

点评 本题考查点在直线上的证明，是基础题，解题时要注意平面的基本性质及推论的合理运用．

练习册系列答案
相关题目
9．已知锐角三角形三边长分别为2，3，a，则a的取值范围为（　　）
A．1＜a＜5B．1＜a＜$\sqrt{13}$C．$\sqrt{5}$＜a＜5D．$\sqrt{5}$＜a＜$\sqrt{13}$
10．设D、E、F分别是△ABC的三边BC、CA、AB上的点，且$\overrightarrow{DC}$=2$\overrightarrow{BD}$，$\overrightarrow{CE}$=2$\overrightarrow{EA}$，$\overrightarrow{AF}$=2$\overrightarrow{FB}$，则$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}$与$\overrightarrow{BC}$（　　）
A．互相垂直B．同向平行
C．反向平行D．既不平行也不垂直
7．函数f（x）=x2+2x-$\frac{{2}^{x}-4}{3}$的零点个数为1．
14．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的虚半轴长为1，离心率e=$\frac{2\sqrt{3}}{3}$，左、右焦点分别为F1，F2．
（1）求双曲线的标准方程；
（2）若过右焦点F2作垂直于x轴的直线1，交双曲线于A、B两点，求|AB|的长．
4．已知△ABC的三内角A，B，C所对三边分别为a，b，c，且sin（A-$\frac{π}{4}$）=$\frac{\sqrt{2}}{10}$．
（1）求tanA的值；
（2）若△ABC的面积S=24，b=10，求a的值．
11．判断下列方程是否表示双曲线？若是，求出a、b、c及焦点坐标．
（1）$\frac{x^2}{4}$-$\frac{y^2}{2}$=1
 （2）$\frac{y^2}{2}$-$\frac{x^2}{2}$=1．
8．与$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1有共同渐近线方程且过点P（$\sqrt{6}，2$）的双曲线标准方程为$\frac{{y}^{2}}{\frac{4}{3}}$-$\frac{{x}^{2}}{3}$=1．
9．选择适当的方法表示下列集合：
（1）小于10的正奇数组成的集合；
（2）直线y=x与抛物线y=x2的交点组成的集合；
（3）不小于2的有理数组成的集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网