题目内容
如图,在 和
和 中,
中, ,若
,若 与
与 的周长之差为
的周长之差为 ,则
,则 的周长为( )
的周长为( )
A.
 B.
B.
 C.
C.
 D.25
D.25
D
解析考点:相似三角形的判定;相似三角形的性质.
分析:由已知中在△ABC和△DBE中, ,我们可以得到△ABC和△DBE相似且相似比等
,我们可以得到△ABC和△DBE相似且相似比等 ,设△ABC的周长为X,根据△ABC与△DBE的周长之差为10cm,我们可以构造一个关于X的方程,解方程即可求出△ABC的周长.
,设△ABC的周长为X,根据△ABC与△DBE的周长之差为10cm,我们可以构造一个关于X的方程,解方程即可求出△ABC的周长.
解:∵在△ABC和△DBE中, ,
,
∴△ABC∽△DBE,相似比等
设△ABC的周长为X,则△DBE的周长为 X
X
又∵△ABC与△DBE的周长之差为10cm
即X- X=10
X=10
解得X=25cm
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
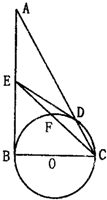 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.  A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长. 中,
中, 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,分别将线段
,分别将线段 和
和 十等分,分点分别记为
十等分,分点分别记为 和
和 ,连接
,连接 ,过
,过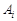 作
作 轴的垂线与
轴的垂线与 。
。
 的方程;
的方程;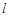 与抛物线E交于不同的两点
与抛物线E交于不同的两点 , 若
, 若 与
与 的面积之比为4:1,求直线
的面积之比为4:1,求直线