题目内容
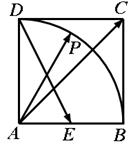
如图,在正方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .分别将线段
.分别将线段![]() 和
和![]() 十等分,分点分别记为
十等分,分点分别记为![]() 和
和![]() ,连结
,连结![]() ,过
,过![]() 做
做![]() 轴的垂线与
轴的垂线与![]() 交于点
交于点![]() .
.
(1)求证:点![]() 都在同一条抛物线上,并求该抛物线
都在同一条抛物线上,并求该抛物线![]() 的方程;
的方程;
(2)过点![]() 做直线
做直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 与
与![]() 的面积比为
的面积比为![]() ,求直线
,求直线![]() 的方程.
的方程.
解:(Ⅰ)依题意,过![]() 且与x轴垂直的直线方程为
且与x轴垂直的直线方程为![]()
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]()
设![]() 坐标为
坐标为![]() ,由
,由 得:
得:![]() ,即
,即![]() ,
,
![]()
![]() 都在同一条抛物线上,且抛物线
都在同一条抛物线上,且抛物线![]() 方程为
方程为![]()
(Ⅱ)依题意:直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
由![]() 得
得![]()
此时![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 恒有两个不同的交点
恒有两个不同的交点![]()
设:![]() ,则
,则
![]()
![]()
![]()
又![]() ,
,![]()
![]()
分别带入![]() ,解得
,解得![]()
直线![]() 的方程为
的方程为![]() ,即
,即![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
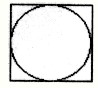 如图,在正方形中撒一粒豆子,则豆子落在正方形内切圆内部的概率为( )
如图,在正方形中撒一粒豆子,则豆子落在正方形内切圆内部的概率为( ) 中,
中, 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,分别将线段
,分别将线段 和
和 十等分,分点分别记为
十等分,分点分别记为 和
和 ,连接
,连接 ,过
,过 作
作 轴的垂线与
轴的垂线与 。
。
 的方程;
的方程; 与抛物线E交于不同的两点
与抛物线E交于不同的两点 , 若
, 若 与
与 的面积之比为4:1,求直线
的面积之比为4:1,求直线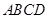 中,
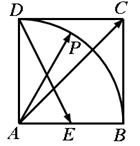
中,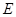 为
为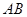 的中点,
的中点,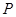 为以
为以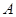 为圆心、
为圆心、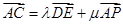 ,则
,则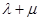 的最小值为
;
的最小值为
;
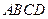 中,
中,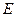 为
为 的中点,
的中点,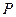 为以
为以 为圆心、
为圆心、 ,则
,则 的最小值为 ;
的最小值为 ;