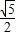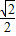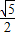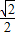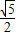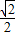Question

设直线x=t与函数f（x）=x²，g（x）=lnx的图象分别交于点M，N，则当MN达到最小时t的值为________．

Answer 1

分析：将两个函数作差，得到函数y=f（x）-g（x），求此函数的最小值，确定对应的自变量x的值，即可得到结论．
解答：设函数y=f（x）-g（x）=x²-lnx（x＞0），求导数得y′=2x-=（x＞0）
令y′＜0，则函数在（0，）上为单调减函数，令y′＞0，则函数在（，+∞）上为单调增函数，
所以当x=时，函数取得最小值为+ln2
所以当MN达到最小时t的值为
故答案为：
点评：本题考查导数知识的运用，解题的关键是构造函数，确定函数的单调性，从而求出函数的最值．