Question

【题目】已知椭圆 =1（a＞b＞0）的右焦点为F2（1，0），点H（2， ）在椭圆上．
（1）求椭圆的方程；
（2）点M在圆x2+y2=b2上，且M在第一象限，过M作圆x2+y2=b2的切线交椭圆于P，Q两点，求证：△PF2Q的周长是定值．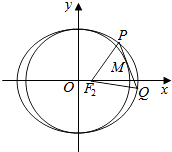

Answer 1

【答案】
（1）解：根据已知，椭圆的左右焦点为分别是F1（﹣1，0），F2（1，0），c=1，

∵ 在椭圆上，∴ ，

∴a=3，b2=a2﹣c2=8，

椭圆的方程是 ；

（2）证明：设P（x1，y1），Q（x2，y2），则 ，

，

∵0＜x1＜3，∴ ，

在圆中，M是切点，

∴ ，

∴ ，

同理|QF2|+|QM|=3，

∴|F2P|+|F2Q|+|PQ|=3+3=6，

因此△PF2Q的周长是定值6．

【解析】1、由椭圆的定义可得 2 a = | H F 1 | + | H F 2 | 再根据即得椭圆的方程。
2、由题意可得根据两点间的距离公式表示出和再由勾股定理求出和根据△PF2Q的周长是定值6