Question

 设f^-1(x)是函数f(x)=(a^x-a^-x)(a＞1)的反函数，则使f^-1(x)＞1成立的x的取值范围为    (    )

    A．(，+∞)  B．(-∞，)    C．(,a)     D．(a，+∞)

 

Answer 1

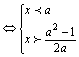  [考场错解]  C  ∵y=  (a^x-a^-x)，∴a^2x-2y·a^x-1=0．a^x==y+．∴x=log_a(y+)，x、y对换．∴f^-1(x)=log_a(x+)(x∈R)又∵f^-1(x)＞1，∴log_a(x+)＞1_x +＞a. ＞a-x∴<x<a．选C.

    [专家把脉]  上面解答错在最后解不等式＞a-x，这一步，因为x+＞a-x应等价于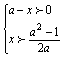或a≤x.错解中只有前面—个不等式组．答案显然错了.

[对症下药]  A  解法1  ∵y=(a^x-a^-x)a^2x-2y·a^x-1=0，a^x==y+

∴x=log_a(y+)．∴f^-1(x)=log_a(x+)(x∈R)．∵f^-1(x)>1

    ∴log_a(x+)>1_x+>a＞a-x＜x＜+∞. 

解法2：利用原函数与反函数的定丈域、值域的关系．原题等价于x>1时，f(x)=(a^x-a^-x)的值域，∴f(x)=(a^x-a^-x)在R上单调递增．∴f(x)＞(a-)=．选A.