题目内容
已知x= 是
是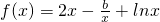 的一个极值点.
的一个极值点.
(Ⅰ)求b的值;
(Ⅱ)求函数f(x)的单调增区间;
(Ⅲ)设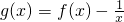 ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
解:(Ⅰ)函数f(x)的定义域为(0,+∞).
f′(x)=2+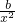 +
+ ,∵x=
,∵x= 是
是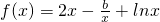 的一个极值点,
的一个极值点,
∴f′( )=0,即 2+4b+2=0,得b=-1,当b=-1时,f′(x)=
)=0,即 2+4b+2=0,得b=-1,当b=-1时,f′(x)= ,
,
当0 时,f′(x)<0;当
时,f′(x)<0;当 时,f′(x)>0,所以x=
时,f′(x)>0,所以x= 为f(x)的极小值点,
为f(x)的极小值点,
所以b=-1.
(Ⅱ)由(Ⅰ)知f′(x)= ,令f′(x)>0得x>
,令f′(x)>0得x> ,
,
∴函数f(x)的单调增区间为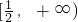 .
.
(Ⅲ)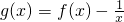 =2x+lnx,
=2x+lnx,
设切点坐标为(x0,2x0+lnx0),则斜率为2+ ,切线方程为:y-2x0-lnx0=(2+
,切线方程为:y-2x0-lnx0=(2+ )(x-x0).
)(x-x0).
∴又切线过点(2,5),∴5-2x0-lnx0=(2+ )(2-x0),
)(2-x0),
即 ,令h(x)=
,令h(x)= ,
,
则h′(x)= =0,得x=2.
=0,得x=2.
h(x)在(0,2)上单调递减,在(2,+∞)上单调递增又∵ ,h(2)=ln2-1<0,
,h(2)=ln2-1<0,
∴h(x)与x轴有两个交点,
故过点(2,5)可作2条曲线y=g(x)的切线.
分析:(Ⅰ)解f′( )=0得到b值,再验证x=
)=0得到b值,再验证x= 为极值点.
为极值点.
(Ⅱ)在定义域内解不等式f′(x)>0即可.
(Ⅲ)设切点坐标,表示出切线方程,转化为方程的解的个数问题,进一步利用数形结合即可求得.
点评:本题考查了应用导数研究函数的极值、单调性问题,难度稍大,注意本题中数形结合思想与转化思想的运用.
f′(x)=2+
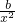 +
+ ,∵x=
,∵x= 是
是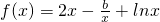 的一个极值点,
的一个极值点,∴f′(
 )=0,即 2+4b+2=0,得b=-1,当b=-1时,f′(x)=
)=0,即 2+4b+2=0,得b=-1,当b=-1时,f′(x)= ,
,当0
 时,f′(x)<0;当
时,f′(x)<0;当 时,f′(x)>0,所以x=
时,f′(x)>0,所以x= 为f(x)的极小值点,
为f(x)的极小值点,所以b=-1.
(Ⅱ)由(Ⅰ)知f′(x)=
 ,令f′(x)>0得x>
,令f′(x)>0得x> ,
,∴函数f(x)的单调增区间为
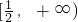 .
.(Ⅲ)
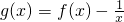 =2x+lnx,
=2x+lnx,设切点坐标为(x0,2x0+lnx0),则斜率为2+
 ,切线方程为:y-2x0-lnx0=(2+
,切线方程为:y-2x0-lnx0=(2+ )(x-x0).
)(x-x0).∴又切线过点(2,5),∴5-2x0-lnx0=(2+
 )(2-x0),
)(2-x0),即
 ,令h(x)=
,令h(x)= ,
,则h′(x)=
 =0,得x=2.
=0,得x=2.h(x)在(0,2)上单调递减,在(2,+∞)上单调递增又∵
 ,h(2)=ln2-1<0,
,h(2)=ln2-1<0,
∴h(x)与x轴有两个交点,
故过点(2,5)可作2条曲线y=g(x)的切线.
分析:(Ⅰ)解f′(
 )=0得到b值,再验证x=
)=0得到b值,再验证x= 为极值点.
为极值点.(Ⅱ)在定义域内解不等式f′(x)>0即可.
(Ⅲ)设切点坐标,表示出切线方程,转化为方程的解的个数问题,进一步利用数形结合即可求得.
点评:本题考查了应用导数研究函数的极值、单调性问题,难度稍大,注意本题中数形结合思想与转化思想的运用.

练习册系列答案
相关题目
 是
是 的一个极值点
的一个极值点 的值;
的值; 的单调增区间;
的单调增区间; ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么? 是
是 的一个极值点.
的一个极值点. ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?