题目内容
(14分)已知函数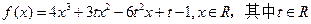 ,
,
(1)当t=1时,求曲线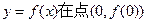 处的切线方程;
处的切线方程;
(2)当t≠0时,求的单调区间;
(3)证明:对任意的 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。
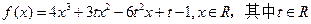 ,
,(1)当t=1时,求曲线
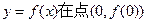 处的切线方程;
处的切线方程;(2)当t≠0时,求的单调区间;
(3)证明:对任意的
 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。(1)当t=1时,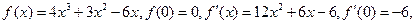
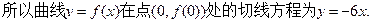
(2)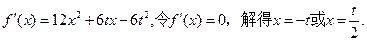

因为t≠0,以下分两种情况讨论:
①若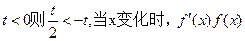 的变化情况如下表:
的变化情况如下表:
所以,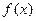 的单调递增区间是
的单调递增区间是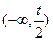 ,(-t,∞)
,(-t,∞) ;
;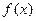 的单调递减区间是
的单调递减区间是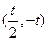 。
。
②若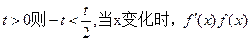 的变化情况如下表:
的变化情况如下表:
所以,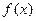 的单调递增区间是(-∞,t),
的单调递增区间是(-∞,t), ;
;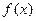 的单调递减区间是
的单调递减区间是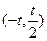 。
。
(3)由(2)可知,当t>0时,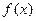 在
在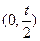 内的单调递减,在
内的单调递减,在 内单调递增,
内单调递增,
以下分两种情况讨论:
①当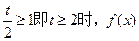 在(0
在(0 ,1)内单调递减,
,1)内单调递减,
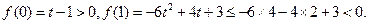
所以对任意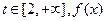 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。
②当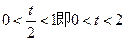 时,
时,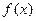 在
在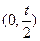 内的单调递减,在
内的单调递减,在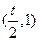 内单调递增,
内单调递增,

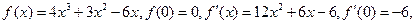
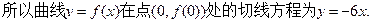
(2)
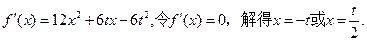

因为t≠0,以下分两种情况讨论:
①若
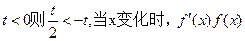 的变化情况如下表:
的变化情况如下表:| x | 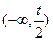 | 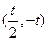 | (-t,∞) |
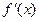 | + | - | + |
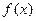 |  |  |  |
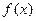 的单调递增区间是
的单调递增区间是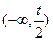 ,(-t,∞)
,(-t,∞) ;
;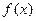 的单调递减区间是
的单调递减区间是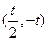 。
。②若
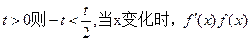 的变化情况如下表:
的变化情况如下表:| x | (-∞,t) | 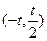 |  |
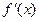 | + | - | + |
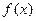 |  |  |  |
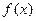 的单调递增区间是(-∞,t),
的单调递增区间是(-∞,t), ;
;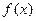 的单调递减区间是
的单调递减区间是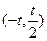 。
。(3)由(2)可知,当t>0时,
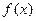 在
在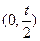 内的单调递减,在
内的单调递减,在 内单调递增,
内单调递增,以下分两种情况讨论:
①当
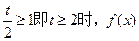 在(0
在(0 ,1)内单调递减,
,1)内单调递减,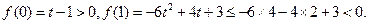
所以对任意
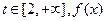 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。②当
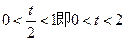 时,
时,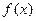 在
在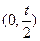 内的单调递减,在
内的单调递减,在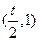 内单调递增,
内单调递增,
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
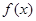 的定义域为(a,b),其导函数
的定义域为(a,b),其导函数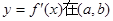 内的图象如图所示,则函数
内的图象如图所示,则函数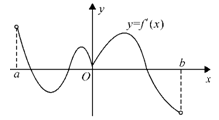
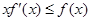 ,若
,若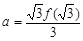 ,
,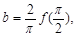
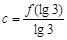 ,则
,则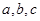 的大小关系是( )
的大小关系是( )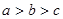
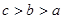
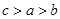
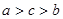
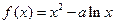 (常数
(常数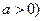 .
.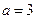 时,求曲线
时,求曲线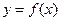 在点
在点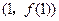 处的切线方程;
处的切线方程;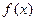 在区间
在区间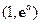 上零点的个数(
上零点的个数(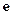 为自然对数的底数).
为自然对数的底数). .
. +
+ +2=0对定义域内的所有
+2=0对定义域内的所有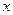 都成立;
都成立; +
+ ,
, -2];
-2];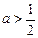 ,函数
,函数 =x2+|(x-
=x2+|(x- (
( )(
)( 为自然对数的底数)
为自然对数的底数) 的极值
的极值 ,
, (
( )
)

 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由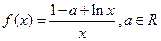 .
.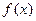 的极值;
的极值;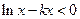 在
在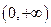 上恒成立,求
上恒成立,求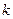 的取值范围;
的取值范围;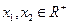 ,且
,且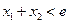 ,求证:
,求证: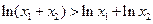 .
.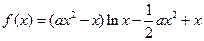 .
.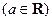 .
.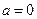 时,求曲线
时,求曲线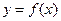 在
在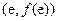 处的切线方程(
处的切线方程(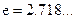 );
);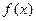 的单调区间.
的单调区间.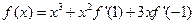 ,则
,则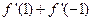 的值为___▲___.
的值为___▲___.