题目内容
如图①,四边形ABCD为等腰梯形,AE⊥DC,AB=AE=| 1 | 3 |

(Ⅰ)求证:平面PAF⊥平面PBE;
(Ⅱ)求直线PF与平面PBC所成角的正弦值.
分析:(I)先证明四边形AEFB为正方形,可证得BE⊥AF;再利用面面垂直的性质,证得线面垂直,再得PE⊥AF,由此可证AF⊥平面PBE,从而证明面面垂直;
(Ⅱ)求出
,平面PBC的一个法向量,利用向量的夹角公式,可求直线PF与平面PBC所成角的正弦值.
(Ⅱ)求出
| PF |
解答: (I)证明:∵EF∥AB,AB=EF=
(I)证明:∵EF∥AB,AB=EF=
CD,
∴四边形AEFB为平行四边形,又AE=AB,AE⊥CD,
∴四边形AEFB为正方形,∴BE⊥AF,
∴平面PAE⊥平面ABCE,PE⊥AE,平面PAE∩平面ABCE=AE,
∴PE⊥平面ABCE,∴PE⊥AF,
又PE∩BE=E,∴AF⊥平面PBE,
∵AF?平面PAF,
∴平面PBE⊥平面PAF;
(Ⅱ)解:建立如图所示的装不下,设AB=4,则P(0,0,4),A(0,4,0),B(4,4,0),C(8,0,0),F(4,0,0),
∴
=(4,0,-4),
=(4,-4,0),
=(4,4,-4),
设
=(x,y,z)为平面PBC的一个法向量,则
,∴可去
=(1,1,2),
∴sinα=|
|=
,
∴直线PF与平面PBC所成角的正弦值为
.
 (I)证明:∵EF∥AB,AB=EF=
(I)证明:∵EF∥AB,AB=EF=| 1 |
| 3 |
∴四边形AEFB为平行四边形,又AE=AB,AE⊥CD,
∴四边形AEFB为正方形,∴BE⊥AF,
∴平面PAE⊥平面ABCE,PE⊥AE,平面PAE∩平面ABCE=AE,
∴PE⊥平面ABCE,∴PE⊥AF,
又PE∩BE=E,∴AF⊥平面PBE,
∵AF?平面PAF,
∴平面PBE⊥平面PAF;
(Ⅱ)解:建立如图所示的装不下,设AB=4,则P(0,0,4),A(0,4,0),B(4,4,0),C(8,0,0),F(4,0,0),
∴
| PF |
| BC |
| PB |
设
| n |
|
| n |
∴sinα=|
| ||||
|
|
| ||
| 6 |
∴直线PF与平面PBC所成角的正弦值为
| ||
| 6 |
点评:本题考查了面面垂直的证明,考查线面角,考查向量知识的运用,正确求出平面的法向量是关键.

练习册系列答案
相关题目
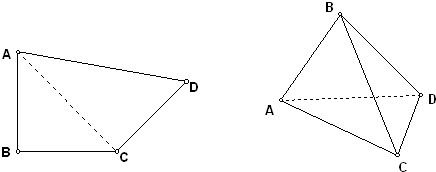 如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直.
如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直. (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2, 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,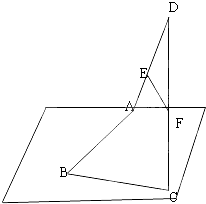 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.