题目内容
已知点
，直线
：
，
为平面上的动点，过点作直线的垂线，垂足为
，且
．
（1）求动点的轨迹
的方程；
（2）已知圆
过定点
，圆心在轨迹上运动，且圆与
轴交于
、
两点，设
，
，求
的最大值．
（1） 
（2）当
时，
的最大值为
解析:
（1）解：设
，则
，
∵
，
∴
．
即
，即
，
所以动点
的轨迹
的方程．
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
（2）解：设圆
的圆心坐标为
，则
． ①
圆的半径为
．
圆的方程为
．
令
，则
，
整理得，
． ②
由①、②解得，
．
不妨设
，
，
∴
，
．
∴
， ③
当
时，由③得，
．
当且仅当
时，等号成立．
当
时，由③得，
．
故当时，
的最大值为
．
练习册系列答案
相关题目
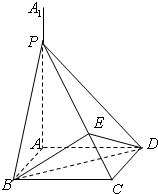已知四边形ABCD是边长为1的正方形，且A1A⊥平面ABCD，P为A1A上一动点，过BD且垂直于PC的平面交PC于E，那么异面直线PC与BD所成的角的度数为
的焦点在
轴上，长轴长为
，离心率为
．
和直线
：
，线段
是椭圆
的值．
.
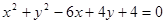过点P且与圆心C的距离为1，求直线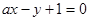
与圆C交于A、B两点，是否存在实数
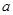，使得过点P(2，0)的直线
垂直平
的焦点在
轴上，长轴长为
，离心率为
．
和直线
：
，线段
是椭圆
的值．
.
过点P且与圆心C的距离为1，求直线
与圆C交于A、B两点，是否存在实数
，使得过点P(2，0)的直线
垂直平