题目内容
(本小题满分12分) 已知曲线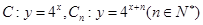 ,从
,从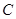 上的点
上的点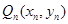 作
作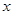 轴的垂线,交
轴的垂线,交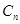 于点
于点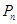 ,再从点
,再从点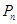 作
作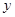 轴的垂线,交
轴的垂线,交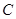 于点
于点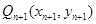 ,
,
设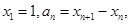
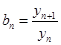 .。
.。
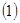 求数列
求数列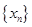 的通项公式;
的通项公式;
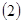 记
记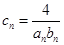 ,数列
,数列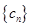 的前
的前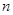 项和为
项和为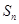 ,试比较
,试比较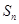 与
与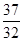 的大小
的大小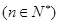 ;
;
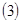 记
记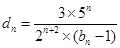 ,数列
,数列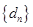 的前
的前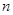 项和为
项和为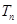 ,试证明:
,试证明: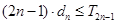 。
。
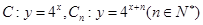 ,从
,从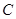 上的点
上的点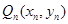 作
作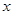 轴的垂线,交
轴的垂线,交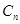 于点
于点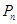 ,再从点
,再从点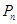 作
作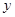 轴的垂线,交
轴的垂线,交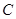 于点
于点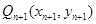 ,
,设
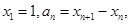
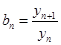 .。
.。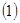 求数列
求数列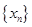 的通项公式;
的通项公式; 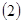 记
记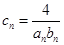 ,数列
,数列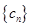 的前
的前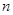 项和为
项和为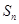 ,试比较
,试比较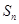 与
与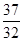 的大小
的大小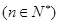 ;
;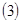 记
记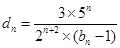 ,数列
,数列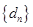 的前
的前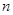 项和为
项和为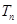 ,试证明:
,试证明: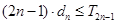 。
。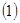

 ;
;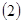
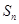 <
<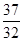 ;(3)
;(3)试题分析:(1)依题意点
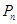 的坐标为
的坐标为 ,
, ,
, ,
,

 ;
;(2)由(1)知,

 ,由
,由 ,
, ,
, ,
, 当
当 时,
时,


 ;.
;.(3)当
 时,有:
时,有:



 ,
,又
 ,
, ,
, .
.所以对任意的
 ,都有
,都有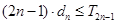 .
.点评:若已知递推公式为
 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。注:①若
 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和; ②若
 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和; ③
 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;④
 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。
练习册系列答案
相关题目
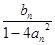 (n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程; ,
, 的等比中项。
的等比中项。 是等差数列;
是等差数列; 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。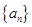 中,
中,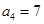 ,且
,且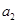 、
、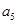 、
、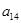 成等比数列.
成等比数列.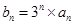 ,求数列
,求数列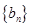 的前
的前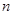 项的和
项的和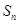 .
.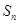 .已知
.已知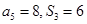 ,则
,则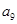 = ( )
= ( )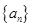 是等差数列,且
是等差数列,且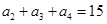 ,则这个数列的前5项和
,则这个数列的前5项和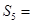 ___________
___________ }的首项
}的首项 =2,
=2, ,数列{
,数列{ .
. }的前
}的前 项和为
项和为 ,且满足
,且满足 }满足
}满足 =1,且
=1,且 ,求数列{
,求数列{ ,求
,求 的前
的前
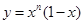 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则
,则 的前n项和是 .
的前n项和是 .