题目内容
设数列 的前
的前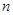 项和
项和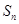 满足
满足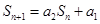 ,其中
,其中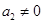 .
.
⑴若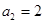 ,求
,求 及
及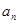 ;
;
⑵若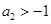 ,求证:
,求证: ,并给出等号成立的充要条件.
,并给出等号成立的充要条件.
(1)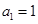 ,
,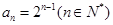 ;(2)当且仅当
;(2)当且仅当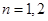 或
或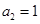 时等号成立.
时等号成立.
解析试题分析:(1)已知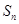 与
与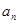 的关系式求出首项和通项,通常都是取特值和写一个递推式相减即可.(2)由(1)得到
的关系式求出首项和通项,通常都是取特值和写一个递推式相减即可.(2)由(1)得到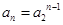 ,分析第1,2项可得后要证的问题等价于
,分析第1,2项可得后要证的问题等价于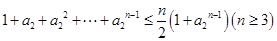 本题是通过利用对称项
本题是通过利用对称项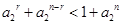 的关系来证明的,该对称项是通过对
的关系来证明的,该对称项是通过对 的范围的讨论得到的. 通过累加后得到
的范围的讨论得到的. 通过累加后得到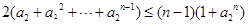 ,然后不等式的两边同时加上
,然后不等式的两边同时加上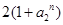 即可得到答案.
即可得到答案.
试题解析:⑴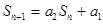 ………①,
………①,
当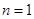 时代入①,得
时代入①,得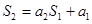 ,解得
,解得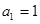 ;
;
由①得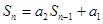 ,两式相减得
,两式相减得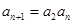 (
(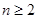 ),故
),故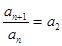 ,故
,故 为公比为2的等比数列,
为公比为2的等比数列,
故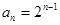 (对
(对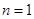 也满足);
也满足);
⑵当 或
或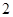 时,显然
时,显然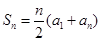 ,等号成立.
,等号成立.
设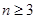 ,
,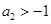 且
且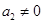 ,由(1)知,
,由(1)知,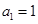 ,
,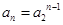 ,所以要证的不等式化为:
,所以要证的不等式化为: 
即证: 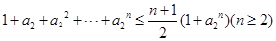
当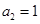 时,上面不等式的等号成立.
时,上面不等式的等号成立.
当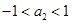 时,
时,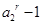 与
与 ,(
,(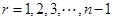 )同为负;
)同为负;
当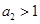 时,
时, 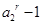 与
与 ,(
,(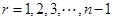 )同为正;
)同为正;
因此当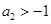 且
且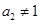 时,总有 (
时,总有 (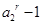 )(
)( )>0,即
)>0,即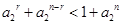 ,(
,(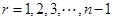 ).
).
上面不等式对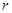 从1到
从1到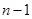 求和得,
求和得,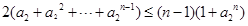 ;
;
由此得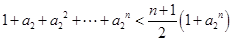 ;
;
综上,当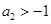 且
且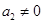 时,有
时,有 ,当且仅当
,当且仅当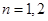 或
或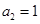 时等号成立.
时等号成立.
考点:1.数列的求和与通项的关系.2.数列中不等式的证明.3.数列的累加法的应用.4.分类的思想.

练习册系列答案
相关题目
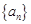 满足:
满足: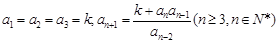 其中
其中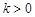 ,数列
,数列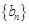 满足:
满足: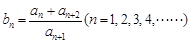
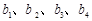 ;
; ,
,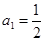 ,且满足
,且满足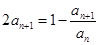 .
. 是等差数列;
是等差数列;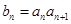 ,求数列
,求数列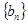 的前n项和
的前n项和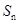 .
.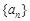 的首项
的首项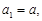 其中
其中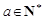 ,
,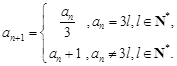 ,令集合
,令集合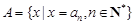 .
.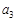 是数列
是数列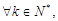 恒有
恒有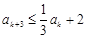 成立;
成立;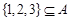 .
.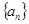 的前
的前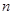 项和为
项和为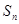 ,且
,且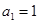 ,
,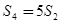 ,数列
,数列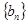 的前
的前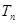 ,满足
,满足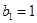 ,
,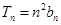 ,
,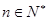 .
. 对所有的
对所有的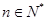 均成立,求实数
均成立,求实数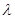 的取值范围.
的取值范围.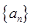 是等比数列,首项
是等比数列,首项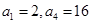 .
.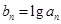 ,证明数列
,证明数列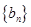 是等差数列并求前n项和
是等差数列并求前n项和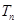 .
.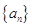 的前
的前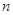 项和为
项和为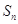 ,
,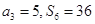 .
. 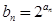 ,求数列
,求数列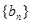 的前
的前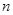 项和
项和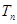 .
.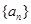 的前
的前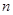 项和为
项和为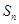 ,已知对任意的
,已知对任意的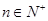 ,点
,点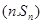 均在函数
均在函数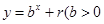 且
且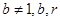 均为常数)的图像上.
均为常数)的图像上.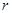 的值;
的值;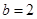 时,记
时,记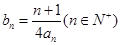 ,求数列
,求数列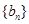 的前
的前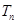 .
. ,数列
,数列 前
前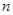 项和
项和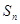 ,
,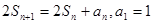 ,数列
,数列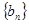 ,满足
,满足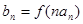 .(Ⅰ)求数列
.(Ⅰ)求数列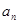 ;
;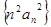 的前
的前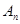 ,数列
,数列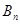 ,证明:
,证明: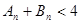 。
。