题目内容
函数y=cos(2x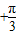 )定义域为[a,b],值域为[-
)定义域为[a,b],值域为[-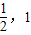 ],则b-a的最大值与最小值之和为( )
],则b-a的最大值与最小值之和为( )A.2π
B.π
C.
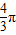
D.
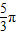
【答案】分析:根据a≤x≤b,可求得2x+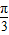 的范围,再结合其值域为[-
的范围,再结合其值域为[-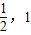 ],可求得满足题意的2x+
],可求得满足题意的2x+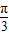 的最大范围与最小范围,从而可求得b-a的最大值与最小值之和.
的最大范围与最小范围,从而可求得b-a的最大值与最小值之和.
解答:解:∵a≤x≤b,
∴2a+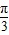 ≤2x+
≤2x+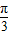 ≤2b+
≤2b+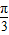 ,
,
又- ≤cos(2x
≤cos(2x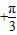 )≤1,
)≤1,
∴2kπ-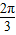 ≤2x
≤2x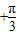 ≤
≤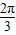 +2kπ或2kπ≤2x
+2kπ或2kπ≤2x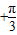 ≤
≤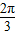 +2kπ(k∈Z),
+2kπ(k∈Z),
∴kπ-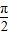 ≤x≤
≤x≤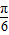 +kπ或kπ-
+kπ或kπ-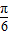 ≤x≤
≤x≤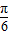 +kπ(k∈Z),
+kπ(k∈Z),
∴(b-a)max=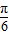 +
+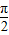 =
=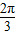 ,(b-a)min=
,(b-a)min=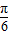 +
+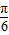 =
=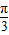 ;
;
∴(b-a)max+(b-a)min=π.
故选B.
点评:本题考查复合三角函数的单调性,突出考查余弦函数的性质与应用,由题意求得满足条件的2x+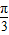 的最大范围与最小范围是关键,也是难点,考查综合分析与理解运用的能力,属于难题.
的最大范围与最小范围是关键,也是难点,考查综合分析与理解运用的能力,属于难题.
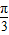 的范围,再结合其值域为[-
的范围,再结合其值域为[-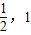 ],可求得满足题意的2x+
],可求得满足题意的2x+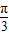 的最大范围与最小范围,从而可求得b-a的最大值与最小值之和.
的最大范围与最小范围,从而可求得b-a的最大值与最小值之和.解答:解:∵a≤x≤b,
∴2a+
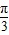 ≤2x+
≤2x+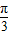 ≤2b+
≤2b+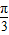 ,
,又-
 ≤cos(2x
≤cos(2x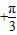 )≤1,
)≤1,∴2kπ-
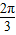 ≤2x
≤2x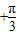 ≤
≤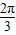 +2kπ或2kπ≤2x
+2kπ或2kπ≤2x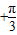 ≤
≤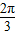 +2kπ(k∈Z),
+2kπ(k∈Z),∴kπ-
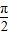 ≤x≤
≤x≤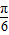 +kπ或kπ-
+kπ或kπ-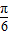 ≤x≤
≤x≤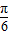 +kπ(k∈Z),
+kπ(k∈Z),∴(b-a)max=
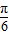 +
+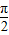 =
=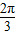 ,(b-a)min=
,(b-a)min=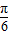 +
+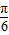 =
=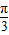 ;
;∴(b-a)max+(b-a)min=π.
故选B.
点评:本题考查复合三角函数的单调性,突出考查余弦函数的性质与应用,由题意求得满足条件的2x+
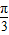 的最大范围与最小范围是关键,也是难点,考查综合分析与理解运用的能力,属于难题.
的最大范围与最小范围是关键,也是难点,考查综合分析与理解运用的能力,属于难题. 
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目