题目内容
如图,从一个半径为 的圆形纸板中切割出一块中间是正方形,四周是以正方形的边为一边的四个正三角形,以此为表面(舍去阴影部分)折叠成一个四棱锥P-ABCD,则该锥体的体积是( )
的圆形纸板中切割出一块中间是正方形,四周是以正方形的边为一边的四个正三角形,以此为表面(舍去阴影部分)折叠成一个四棱锥P-ABCD,则该锥体的体积是( )
A.

B.

C.

D.

【答案】分析:由折叠前的图形知,底面正方形ABCD,侧面正△PAB,斜高PM,AB:PM= ,由
,由 =
= ,得AB=2m,PM=
,得AB=2m,PM= ,从而得出四棱锥的高和体积.
,从而得出四棱锥的高和体积.
解答: 解:如图,
解:如图,
在四棱锥P-ABCD中,底面正方形ABCD,侧面正△PBC,斜高PM,AB:PM= ,
,
且 =
= ,则AB=2m,h=
,则AB=2m,h= =
= ,
,
所以,该四锥体的体积为:V= •S正方形ABCD•h=
•S正方形ABCD•h= •(2m)2•
•(2m)2• =
= .
.
故答案为:A
点评:本题是通过四棱锥的侧面展开图求其体积,关键是由斜高,高和斜高在底面的射影组成Rt△,求出高,从而求得体积.
 ,由
,由 =
= ,得AB=2m,PM=
,得AB=2m,PM= ,从而得出四棱锥的高和体积.
,从而得出四棱锥的高和体积.解答:
 解:如图,
解:如图,在四棱锥P-ABCD中,底面正方形ABCD,侧面正△PBC,斜高PM,AB:PM=
 ,
,且
 =
= ,则AB=2m,h=
,则AB=2m,h= =
= ,
,所以,该四锥体的体积为:V=
 •S正方形ABCD•h=
•S正方形ABCD•h= •(2m)2•
•(2m)2• =
= .
.故答案为:A
点评:本题是通过四棱锥的侧面展开图求其体积,关键是由斜高,高和斜高在底面的射影组成Rt△,求出高,从而求得体积.

练习册系列答案
相关题目
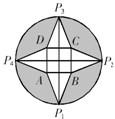 如图,从一个半径为(1+
如图,从一个半径为(1+| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|


 )m的圆形纸板中切割出一块中间是正方形,四周是以正方形的边为一边的四个正三角形,以此为表面(舍去阴影部分)折叠成一个四棱锥P-ABCD,则该锥体的体积是
)m的圆形纸板中切割出一块中间是正方形,四周是以正方形的边为一边的四个正三角形,以此为表面(舍去阴影部分)折叠成一个四棱锥P-ABCD,则该锥体的体积是
 m3
m3 m3
m3 m3
m3 m3
m3