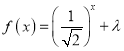题目内容
【题目】已知圆![]() ,椭圆
,椭圆![]() (
(![]() )的短轴长等于圆
)的短轴长等于圆![]() 半径的
半径的![]() 倍,
倍,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切,证明:
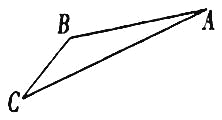
相切,证明:![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ; (2)证明见解析.
; (2)证明见解析.
【解析】
(1)根据椭圆的几何性质即可求出![]() 的方程;
的方程;
(2)法一,分直线斜率不存在和存在两种情况,求出点坐标利用向量数量积即可证明,法二,分和![]() 轴平行和不平行两种情况,后和法一一样.
轴平行和不平行两种情况,后和法一一样.
(1)因为圆![]() 的半径为
的半径为![]() ,
,
所以![]() 的短轴长为
的短轴长为![]() ,
,
所以![]() ,解得
,解得![]() .
.
因为![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ①,
①,
又因为![]() ,所以
,所以![]() ②,
②,
联立①② ,解得![]() ,
,
所以所求![]() 的方程为
的方程为![]()
(2)证明:证法一:①当直线![]() 斜率不存在时, 直线
斜率不存在时, 直线![]() 的方程为
的方程为![]() .
.
当![]() 时,
时,![]()
所以![]()
当![]() 时,
时,![]()
所以![]() ,
,
综上,![]()
所以![]() 为直角三角形.
为直角三角形.
②当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]()
![]() 直线
直线![]() 与圆相切,
与圆相切,![]()
即![]() ,
,
由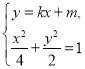 得,
得,![]() ,
,
所以![]()
所以![]()
![]()
![]()
![]()
![]()
所以![]()
综上所述:![]() 所以
所以![]() 为直角三角形.
为直角三角形.
证法二:①当直线方程为![]() 时,
时,
![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
②当直线方程为![]() 时,
时,![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
③当直线![]() 不与
不与![]() 轴平行时,设其方程为
轴平行时,设其方程为![]()
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]()
由 得,
得,![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
综上所述: ![]() 为直角三角形.
为直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目