题目内容
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“平底型”函数.
上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为
是否为![]() 上的“平底型”函数?
上的“平底型”函数?
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
【答案】(1) ![]() 是“平底型”函数,
是“平底型”函数, ![]() 不是“平底型”函数;(2)
不是“平底型”函数;(2) ![]() .
.
【解析】
试题分析:(1)分区间去掉绝对值符号,分别讨论![]() 与
与![]() 的性质与“平底型”函数定义对照即可;
的性质与“平底型”函数定义对照即可;
(2) 函数![]() 是区间
是区间![]() 上的“平底型”函数等价于存在区间
上的“平底型”函数等价于存在区间![]() 和常数
和常数![]() ,使得
,使得![]() 恒成立,即
恒成立,即![]() 恒成立,亦即
恒成立,亦即 ,解之即可.
,解之即可.
试题解析: (1)对于函数![]() ,当
,当![]() 时,
时,![]() .
.
当![]() 或
或![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 是“平底型”函数.
是“平底型”函数.
对于函数![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以不存在闭区间![]() ,使当
,使当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 不是“平底型”函数.
不是“平底型”函数.
(2)因为函数![]() 是区间
是区间![]() 上的“平底型”函数,则
上的“平底型”函数,则
存在区间![]() 和常数
和常数![]() ,使得
,使得![]() 恒成立.
恒成立.
所以![]() 恒成立,即
恒成立,即 解得
解得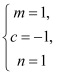 或
或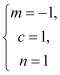 .
.
当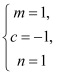 时,
时,![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 恒成立,此时,
恒成立,此时,![]() 是区间
是区间![]() 上的“平底型”函数.
上的“平底型”函数.
当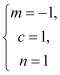 时,
时,![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 恒成立,此时,
恒成立,此时,![]() 不是区间
不是区间![]() 上的“平底型”函数.
上的“平底型”函数.
综上分析,![]() 为所求.
为所求.

练习册系列答案
相关题目
