题目内容
9.已知角α的终边经过点(-2,1),则cos2α=( )| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
分析 由条件利用任意角的三角函数的定义求得cosα的值,再利用二倍角的余弦公式求得cos2α的值.
解答 解:角α的终边经过点(-2,1),∴x=-2 r=$\sqrt{5}$,cosα=$\frac{x}{r}$=-$\frac{2}{\sqrt{5}}$,
则cos2α=2cos2α-1=2×$\frac{4}{5}$-1=$\frac{3}{5}$,
故选:B.
点评 本题主要考查任意角的三角函数的定义,二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
20.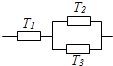 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{15}{32}$ | D. | $\frac{17}{32}$ |
4.为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人.
(Ⅰ)根据以上数据建立2×2列联表;
(Ⅱ)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ (n=a+b+c+d)
(Ⅰ)根据以上数据建立2×2列联表;
(Ⅱ)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
14.三棱锥P-ABC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA=3,AB=BC=2,则球O的表面积为( )
| A. | 13π | B. | 17π | C. | 52π | D. | 68π |
18.设命题甲:关于x的不等式x2+2ax+4≥0对一切x∈R恒成立,命题乙:设函数f(x)=loga(x-a+2)在区间(1,+∞)上恒为正值,那么甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |