题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的正整数
,对任意的正整数![]() ,都有
,都有![]() 成立,记
成立,记![]() 。
。
(I)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(II)设数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对任意正整数
,求证:对任意正整数![]() 都有
都有![]() ;
;
解:(I)当![]() 时,
时,![]()
又![]()
![]()
∴数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴![]() ,
, …………………………………3分
…………………………………3分
(II)不存在正整数![]() ,使得
,使得![]() 成立。
成立。
证明:由(I)知
![]()
∴当n为偶数时,设![]()
∴![]()
当n为奇数时,设![]()
∴![]()
∴对于一切的正整数n,都有![]()
∴不存在正整数![]() ,使得
,使得![]() 成立。 …………………………………8分
成立。 …………………………………8分
(III)由![]() 得
得
![]()
又![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,

…………………………………14分

练习册系列答案
相关题目
 的前
的前 的前
的前 项和为
项和为 ,对任意的正整数
,对任意的正整数 成立,记
成立,记 。
。 的通项公式;
的通项公式; ,设数列
,设数列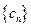 的前
的前 ,求证:对任意正整数
,求证:对任意正整数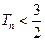 ;
; 。已知正实数
。已知正实数 满足:对任意正整数
满足:对任意正整数 恒成立,求
恒成立,求 的前
的前 项和为
项和为 ,对
,对 ,都有
,都有 成立,
成立, ,试求数列
,试求数列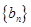 的前
的前 .
. 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 在函数
在函数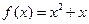 的图象上.
的图象上. 的表达式;
的表达式; ),(
),( ,
, ),(
),( ,
, ,
, ),(
),(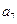 ,
,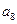 ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
,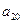 );(
);( ),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;w*w^w.k&s#5@u.c~o*m
的值;w*w^w.k&s#5@u.c~o*m 为数列
为数列 的前
的前 ,使得不等式
,使得不等式 对一切
对一切