Question

【题目】如果存在函数（为常数），使得对函数定义域内任意都有成立，那么称为函数的一个“线性覆盖函数”．给出如下四个结论：

①函数存在“线性覆盖函数”；

②对于给定的函数，其“线性覆盖函数”可能不存在，也可能有无数个；

③为函数的一个“线性覆盖函数”；

④若为函数的一个“线性覆盖函数”，则

其中所有正确结论的序号是___________.

Answer 1

【答案】②③.

【解析】

根据题中提供的定义，对每一个选项通过证明或找反例分析对错，从而解得正确选项.

解：选项①：假设存在，为函数的一个“线性覆盖函数”，此时显然不成立，只有才有可能使得对函数定义域内任意都有成立，即，而事实上，增长的速度比要快很多，当时，的函数值一定会大于的函数值，故选项①不成立；

选项②：如函数，则就是函数的一个“线性覆盖函数”，且有无数个，再如①中的就没有“线性覆盖函数”，所以命题②正确；

选项③：设，

则，

令，解得，

当时，，函数为单调增函数；

当时，，函数为单调减函数；

所以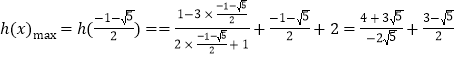

，

所以在上恒成立，故满足定义，选项③正确；

选项④：若为函数的一个“线性覆盖函数”，

则 在R上恒成立，

即在R上恒成立，

故，

因为开口向下，对称轴为，

所以当时，，

所以，所以选项④错误，

故本题选择②③.