题目内容
已知数列 满足 ,
满足 ,
证明: ,(
,( )
)
见解析
解析试题分析:本小题根据 可知
可知
从而可知 是以2为首项,2为公比的等比数列,从而可求出
是以2为首项,2为公比的等比数列,从而可求出
 ,然后再根据
,然后再根据
然后叠加证明即可.
证明:




 考点:等比数列的通项公式,利用不等式的放缩证明不等式.
考点:等比数列的通项公式,利用不等式的放缩证明不等式.
点评:解本题的入口是构造等比数列求出{an}的通项公式,一般地对于 ,可采用构造等比数列求通项,然后证明不等式可考虑采用不等式的放缩法证明即可.
,可采用构造等比数列求通项,然后证明不等式可考虑采用不等式的放缩法证明即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列 的前
的前 项和为
项和为 ,则
,则 的值是( )
的值是( )
A. | B.73 | C. | D.15 |
 ( )
( )
A. | B. |
C. | D. |
 是等比数列
是等比数列 的前
的前 项和,且
项和,且 ,
, .
. ;
; ,求数列
,求数列 的前
的前 .
.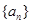 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
. 为等差数列,并求
为等差数列,并求 的前n项和为
的前n项和为 ,求使得
,求使得 的最小正整数
的最小正整数 .
. 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列, 为
为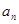 及
及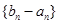 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列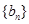 的通项公式及其前n项和
的通项公式及其前n项和
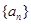 中,
中,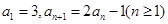
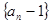 是等比数列;
是等比数列; ,求证:数列
,求证:数列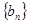 的前
的前 项和
项和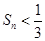 .
.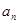 与
与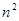 的大小(
的大小( )。
)。 的前
的前 项和为
项和为 且
且 .
. ;
; 问是否存在实数
问是否存在实数 ,使得对于任意的
,使得对于任意的 都有
都有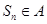 ? 若存在,求出
? 若存在,求出