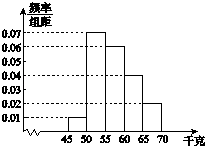
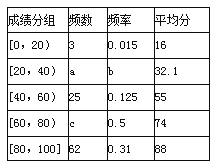
题目内容
【题目】【2017南通二模19】已知函数![]() ,
,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数![]() 在x
在x![]() 1处的切线方程;
1处的切线方程;
(2)若存在![]()
![]() ,使得
,使得![]() 成立,其中
成立,其中![]() 为常数,
为常数,
求证:![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】见解析
【解析】解:(1)因为![]() ,所以
,所以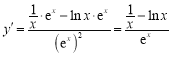 ,故
,故![]() .
.
所以函数![]() 在x
在x![]() 1处的切线方程为
1处的切线方程为![]() ,
,
即![]() .
.
(2)由已知等式![]() 得
得![]() .
.
记![]() ,则
,则![]() .
.
假设![]() .
.
①若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上为单调增函数.
上为单调增函数.
又![]() ,所以
,所以![]() ,与
,与![]() 矛盾.
矛盾.
②若![]() ,记
,记![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调增函数;
上为单调增函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调减函数.
上为单调减函数.
所以![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上为单调增函数.
上为单调增函数.
又![]() ,所以
,所以![]() ,与
,与![]() 矛盾.
矛盾.
综合①②,假设不成立,所以![]() .9分
.9分
(3)由![]() 得
得![]() .
.
记![]() ,
,![]() ,
,
则![]() .
.
①当![]() 时,因为
时,因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上为单调增函数,所以
上为单调增函数,所以![]() ,
,
故原不等式恒成立.1
②法一:
当![]() 时,由(2)知
时,由(2)知![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为单调减函数,
为单调减函数,
所以![]() ,不合题意.
,不合题意.
法二:
当![]() 时,一方面
时,一方面![]() .
.
另一方面,![]() ,
,![]() .
.
所以![]() ,使
,使![]() ,又
,又![]() 在
在![]() 上为单调减函数,
上为单调减函数,
所以当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为单调减函数,
上为单调减函数,
所以![]() ,不合题意.
,不合题意.
综上,![]() .1
.1

练习册系列答案
相关题目
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.