Question

【题目】【2017扬州一模20】已知函数，其中函数，．

（1）求函数在处的切线方程；

（2）当时，求函数在上的最大值；

（3）当时，对于给定的正整数，问函数是否有零点？请说明理由．（参考数据）

Answer 1

【答案】见解析

【解析】解：(1)，故，

所以切线方程为，即

（2），故，

令，得或.

①当,即时，在上递减，在上递增，

所以,

由于，，故，

所以;

②当,即时，在上递增，上递减，在上递增，

所以，

由于，，故，7分

所以;

综上得，

（3）结论：当时，函数无零点；当时，函数有零点9分

理由如下：

①当时，实际上可以证明：．

方法一：直接证明的最小值大于0，可以借助虚零点处理．

，显然可证在上递增，

因为，，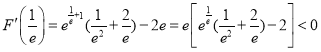

所以存在，使得，

所以当时，递减；当时，递增，

所以，其中，

而递减，所以，

所以，所以命题得证。

方法二：转化为证明，下面分别研究左右两个函数．

令，则可求得，

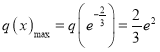令，则可求得，所以命题得证。1

方法三：先放缩，再证明．

可先证明不等式（参考第1小题，过程略），所以只要证，

令，则可求得，

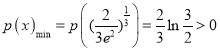所以命题得证．

②当时，，

此时，，

下面证明，可借助结论处理，首先证明结论：

令，则，故，

所以在上递增，所以，

所以在上递增，所以，得证。

借助结论得，

所以，又因为函数连续，

所以在上有零点.